
【题目】如图(1)所示,在直角梯形ABCD中, ![]() ,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图(2)所示.
,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图(2)所示. 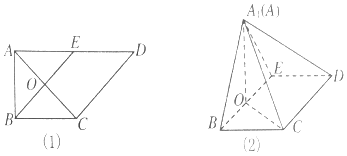
(1)证明:CD⊥平面A1OC;
(2)若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD所成锐二面角的余弦值.
【答案】
(1)证明:在图(1)中,因为 ![]() ,E是AD的中点,且
,E是AD的中点,且 ![]() ,
,
所以BE⊥AC,BE∥CD,
即在图(2)中,BE⊥OA1,BE⊥OC,又OA1∩OC=O,OA1平面A1OC,OC平面A1OC,
从而BE⊥平面A1OC,又BE∥CD,所以CD⊥平面A1OC
(2)解:由已知,平面A1BE⊥平面BCDE,且交线为BE,
又由(1)知,BE⊥OA1,所以OA1⊥平面BCDE,
如图,以O为原点,OB,OC,OA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
设 ![]() ,所以
,所以 ![]() ,
,
得 ![]() .
.
设平面A1BC的法向量 ![]() ,平面A1CD的法向量
,平面A1CD的法向量 ![]() ,
,
平面A1BC与平面A1CD的夹角为θ,
则 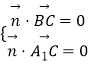 得
得 ![]() ,取
,取 ![]() ,同理,取
,同理,取 ![]() ,
,
从而 ![]() ,
,
即平面A1BC与平面A1CD所成锐二面角的余弦值为 ![]() .
.
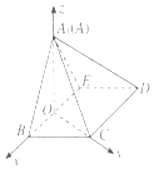
【解析】(1)BE⊥平面A1OC,又BE∥CD,即可证明:CD⊥平面A1OC;(2)若平面A1BE⊥平面BCDE,以O为原点,OB,OC,OA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,求出平面的法向量,即可求平面A1BC与平面A1CD所成锐二面角的余弦值.
【考点精析】掌握直线与平面垂直的判定是解答本题的根本,需要知道一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图四棱锥P﹣ABCD底面是矩形,PA⊥平面ABCD,PA=AB=1, ![]() ,E是BC上的点,
,E是BC上的点, 
(1)试确定E点的位置使平面PED⊥平面PAC,并证明你的结论;
(2)在条件(1)下,求二面角B﹣PE﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣9x,函数g(x)=3x2+a. (Ⅰ)已知直线l是曲线y=f(x)在点(0,f(0))处的切线,且l与曲线y=g(x)相切,求a的值;
(Ⅱ)若方程f(x)=g(x)有三个不同实数解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】锐角△ABC中,其内角A、B满足:2cosA=sinB﹣ ![]() cosB.
cosB.
(1)求角C的大小;
(2)D为AB的中点,CD=1,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则剩余部分体积与原四棱锥体积的比值为( )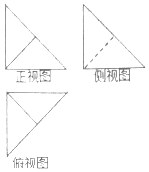
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《张丘建算经》是我国南北朝时期的一部重要数学著作,书中系统的介绍了等差数列,同类结果在三百多年后的印度才首次出现.书中有这样一个问题,大意为:某女子善于织布,后一天比前一天织的快,而且每天增加的数量相同,已知第一天织布5尺,一个月(按30天计算)总共织布390尺,问每天增加的数量为多少尺?该问题的答案为( )
A.![]() 尺
尺
B.![]() 尺
尺
C.![]() 尺
尺
D.![]() 尺
尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为 ![]() (θ为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ=﹣2.
(θ为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ=﹣2.
(Ⅰ)求C1和C2在直角坐标系下的普通方程;
(Ⅱ)已知直线l:y=x和曲线C1交于M,N两点,求弦MN中点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】艾萨克牛顿(1643年1月4日﹣1727年3月31日)英国皇家学会会长,英国著名物理学家,同时在数学上也有许多杰出贡献,牛顿用“作切线”的方法求函数f(x)零点时给出一个数列{xn}:满足 ![]() ,我们把该数列称为牛顿数列.如果函数f(x)=ax2+bx+c(a>0)有两个零点1,2,数列{xn}为牛顿数列,设
,我们把该数列称为牛顿数列.如果函数f(x)=ax2+bx+c(a>0)有两个零点1,2,数列{xn}为牛顿数列,设 ![]() ,已知a1=2,xn>2,则{an}的通项公式an= .
,已知a1=2,xn>2,则{an}的通项公式an= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的图象在点(x0 , f(x0))处的切线方程l:y=g(x),若函数f(x)满足x∈I(其中I为函数f(x)的定义域),当x≠x0时,[f(x)﹣g(x)](x﹣x0)>0恒成立,则称x0为函数f(x)的“穿越点”.已知函数f(x)=lnx﹣ ![]() x2﹣
x2﹣ ![]() 在(0,e]上存在一个“穿越点”,则a的取值范围为( )
在(0,e]上存在一个“穿越点”,则a的取值范围为( )
A.[ ![]() ,+∞)??
,+∞)??
B.(﹣1, ![]() ]??
]??
C.[﹣ ![]() ,1)??
,1)??
D.(﹣∞,﹣ ![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com