
【题目】艾萨克牛顿(1643年1月4日﹣1727年3月31日)英国皇家学会会长,英国著名物理学家,同时在数学上也有许多杰出贡献,牛顿用“作切线”的方法求函数f(x)零点时给出一个数列{xn}:满足 ![]() ,我们把该数列称为牛顿数列.如果函数f(x)=ax2+bx+c(a>0)有两个零点1,2,数列{xn}为牛顿数列,设
,我们把该数列称为牛顿数列.如果函数f(x)=ax2+bx+c(a>0)有两个零点1,2,数列{xn}为牛顿数列,设 ![]() ,已知a1=2,xn>2,则{an}的通项公式an= .
,已知a1=2,xn>2,则{an}的通项公式an= .
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知{an}满足a1=1,an+an+1=( ![]() )n(n∈N*),Sn=a1+4a2+42a3+…+4n﹣1an , 则5Sn﹣4nan=( )
)n(n∈N*),Sn=a1+4a2+42a3+…+4n﹣1an , 则5Sn﹣4nan=( )
A.n﹣1
B.n
C.2n
D.n2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1)所示,在直角梯形ABCD中, ![]() ,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图(2)所示.
,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图(2)所示. 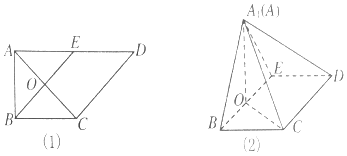
(1)证明:CD⊥平面A1OC;
(2)若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知U=R,M={x|﹣l≤x≤2},N={x|x≤3},则(UM)∩N=( )
A.{x|2≤x≤3}
B.{x|2<x≤3}
C.{x|x≤﹣1,或2≤x≤3}
D.{x|x<﹣1,或2<x≤3}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆E: ![]() ,点P(0,1)在短轴CD上,且
,点P(0,1)在短轴CD上,且 ![]()
(Ⅰ) 求椭圆E的方程及离心率;
(Ⅱ) 设O为坐标原点,过点P的动直线与椭圆交于A,B两点.是否存在常数λ,使得 ![]() 为定值?若存在,求λ的值;若不存在,请说明理由.
为定值?若存在,求λ的值;若不存在,请说明理由.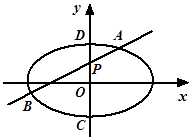
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若a1=1,对任意的n∈N* , 都有an>0,且nan+12﹣(2n﹣1)an+1an﹣2an2=0设M(x)表示整数x的个位数字,则M(a2017)= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com