
【题目】如图,椭圆E: ![]() ,点P(0,1)在短轴CD上,且
,点P(0,1)在短轴CD上,且 ![]()
(Ⅰ) 求椭圆E的方程及离心率;
(Ⅱ) 设O为坐标原点,过点P的动直线与椭圆交于A,B两点.是否存在常数λ,使得 ![]() 为定值?若存在,求λ的值;若不存在,请说明理由.
为定值?若存在,求λ的值;若不存在,请说明理由.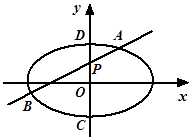
【答案】解:(Ⅰ)由已知,点C,D的坐标分别为(0,﹣b),(0,b).
又点P的坐标为(0,1),且 ![]() ,即1﹣b2=﹣2,
,即1﹣b2=﹣2,
解得b2=3.
∴椭圆E方程为 ![]() .
.
∵c= ![]() =1,∴离心率e=
=1,∴离心率e= ![]() ;
;
(Ⅱ)当直线AB的斜率存在时,设直线AB的方程为y=kx+1,A,B的坐标分别为(x1 , y1),(x2 , y2).
联立 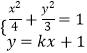 ,得(4k2+3)x2+8kx﹣8=0.
,得(4k2+3)x2+8kx﹣8=0.
其判别式△>0,
x1+x2= ![]() ,x1x2=
,x1x2= ![]() .
.
从而, ![]() =x1x2+y1y2+λ[x1x2+(y1﹣1)(y2﹣1)]
=x1x2+y1y2+λ[x1x2+(y1﹣1)(y2﹣1)]
=(1+λ)(1+k2)x1x2+k(x1+x2)+1
= ![]() =
= ![]() ﹣2λ﹣3,
﹣2λ﹣3,
当λ=2时, ![]() ﹣2λ﹣3=﹣7,
﹣2λ﹣3=﹣7,
即 ![]() =﹣7为定值.
=﹣7为定值.
当直线AB斜率不存在时,直线AB即为直线CD,
此时 ![]() =
= ![]() =﹣3﹣4=﹣7,
=﹣3﹣4=﹣7,
故存在常数λ=2,使得 ![]() 为定值﹣7
为定值﹣7
【解析】(Ⅰ)由已知可得点C,D的坐标分别为(0,﹣b),(0,b).结合 ![]() 列式求得b,则椭圆方程可求,进一步求出c可得椭圆的离心率;(Ⅱ)当直线AB的斜率存在时,设直线AB的方程为y=kx+1,A,B的坐标分别为(x1 , y1),(x2 , y2).联立直线方程和椭圆方程,利用根与系数的关系可得A,B横坐标的和与积
列式求得b,则椭圆方程可求,进一步求出c可得椭圆的离心率;(Ⅱ)当直线AB的斜率存在时,设直线AB的方程为y=kx+1,A,B的坐标分别为(x1 , y1),(x2 , y2).联立直线方程和椭圆方程,利用根与系数的关系可得A,B横坐标的和与积 ![]() ,可知当λ=2时,
,可知当λ=2时, ![]() =﹣7为定值.当直线AB斜率不存在时,直线AB即为直线CD,仍有
=﹣7为定值.当直线AB斜率不存在时,直线AB即为直线CD,仍有 ![]() =
= ![]() =﹣3﹣4=﹣7,故存在常数λ=2,使得
=﹣3﹣4=﹣7,故存在常数λ=2,使得 ![]() 为定值﹣7.
为定值﹣7.


科目:高中数学 来源: 题型:
【题目】《张丘建算经》是我国南北朝时期的一部重要数学著作,书中系统的介绍了等差数列,同类结果在三百多年后的印度才首次出现.书中有这样一个问题,大意为:某女子善于织布,后一天比前一天织的快,而且每天增加的数量相同,已知第一天织布5尺,一个月(按30天计算)总共织布390尺,问每天增加的数量为多少尺?该问题的答案为( )
A.![]() 尺
尺
B.![]() 尺
尺
C.![]() 尺
尺
D.![]() 尺
尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l: 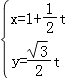 (t为参数),曲线C1:
(t为参数),曲线C1: ![]() (θ为参数).
(θ为参数).
(Ⅰ)设l与C1相交于A,B两点,求|AB|;
(Ⅱ)若把曲线C1上各点的横坐标压缩为原来的 ![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的 ![]() 倍,得到曲线C2 , 设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.
倍,得到曲线C2 , 设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】艾萨克牛顿(1643年1月4日﹣1727年3月31日)英国皇家学会会长,英国著名物理学家,同时在数学上也有许多杰出贡献,牛顿用“作切线”的方法求函数f(x)零点时给出一个数列{xn}:满足 ![]() ,我们把该数列称为牛顿数列.如果函数f(x)=ax2+bx+c(a>0)有两个零点1,2,数列{xn}为牛顿数列,设
,我们把该数列称为牛顿数列.如果函数f(x)=ax2+bx+c(a>0)有两个零点1,2,数列{xn}为牛顿数列,设 ![]() ,已知a1=2,xn>2,则{an}的通项公式an= .
,已知a1=2,xn>2,则{an}的通项公式an= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高三年级随机抽取一个班,对该班50名学生的高校招生体检表中的视力情况进行统计,其频率分布直方图如图所示.若某高校A专业对视力的要求在0.9以上,则该班学生中能报A专业的人数为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)= ![]() +g(x).
+g(x).
(1)试判断g(x)的单调性;
(2)若f(x)在区间(0,1)上有极值,求实数a的取值范围;
(3)当a>0时,若f(x)有唯一的零点x0 , 试求[x0]的值.(注:[x]为取整函数,表示不超过x的最大整数,如[0.3]=0,[2.6]=2,[﹣1.4]=﹣2;以下数据供参考:ln2=0.6931,ln3=1.099,ln5=1.609,ln7=1.946)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一缉私艇巡航至距领海边界线l(一条南北方向的直线)3.8海里的A处,发现在其北偏东30°方向相距4海里的B处有一走私船正欲逃跑,缉私艇立即追击.已知缉私艇的最大航速是走私船最大航速的3倍.假设缉私艇和走私船均按直线方向以最大航速航行.(参考数据: ![]() °
° ![]() ,
, ![]() )
)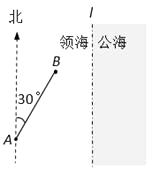
(1)若走私船沿正东方向逃离,试确定缉私艇的追击方向,使得用最短时间在领海内拦截成功;
(2)问:无论走私船沿何方向逃跑,缉私艇是否总能在领海内成功拦截?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且Sn=﹣1+2an(Ⅰ)求{an}的通项公式;
(Ⅱ)若bn=log2an+1 , 且数列{bn}的前n项和为Tn , 求 ![]() +…+
+…+ ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com