
【题目】一缉私艇巡航至距领海边界线l(一条南北方向的直线)3.8海里的A处,发现在其北偏东30°方向相距4海里的B处有一走私船正欲逃跑,缉私艇立即追击.已知缉私艇的最大航速是走私船最大航速的3倍.假设缉私艇和走私船均按直线方向以最大航速航行.(参考数据: ![]() °
° ![]() ,
, ![]() )
)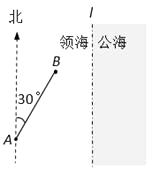
(1)若走私船沿正东方向逃离,试确定缉私艇的追击方向,使得用最短时间在领海内拦截成功;
(2)问:无论走私船沿何方向逃跑,缉私艇是否总能在领海内成功拦截?并说明理由.
【答案】
(1)
解:(1)设缉私艇在 ![]() 处与走私船相遇(如图甲),
处与走私船相遇(如图甲),
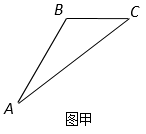
依题意, ![]() .
.
在△ ![]() 中,由正弦定理得,
中,由正弦定理得,
![]()
![]()
![]() .
.
因为 ![]() °
° ![]() ,所以
,所以 ![]() °.
°.
从而缉私艇应向北偏东 ![]() 方向追击.
方向追击.
在△ ![]() 中,由余弦定理得,
中,由余弦定理得,
![]() ,
,
解得 ![]()
![]() .
.
又B到边界线l的距离为 ![]() .
.
因为 ![]() ,所以能在领海上成功拦截走私船.
,所以能在领海上成功拦截走私船.
答:缉私艇应向北偏东 ![]() 方向追击;
方向追击;
(2)
解:如图乙,以 ![]() 为原点,正北方向所在的直线为
为原点,正北方向所在的直线为 ![]() 轴建立平面直角坐标系
轴建立平面直角坐标系 ![]() .
.
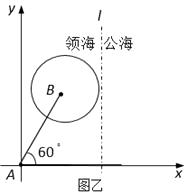
则 ![]() ,设缉私艇在
,设缉私艇在 ![]() 处(缉私艇恰好截住走私船的位置)与走私船相遇,则
处(缉私艇恰好截住走私船的位置)与走私船相遇,则 ![]() ,即
,即 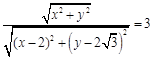 .
.
整理得, ![]() ,
,
所以点 ![]() 的轨迹是以点
的轨迹是以点 ![]() 为圆心,
为圆心, ![]() 为半径的圆.
为半径的圆.
因为圆心 ![]() 到领海边界线
到领海边界线 ![]() :
: ![]() 的距离为1.55,大于圆半径
的距离为1.55,大于圆半径 ![]() ,
,
所以缉私艇能在领海内截住走私船.
答:缉私艇总能在领海内成功拦截走私船.
【解析】(1) 假设在C点能拦截,由BC、AC关系算出∠BAC,再由余弦定理算出BC判断BC与B到边界的距离。(2)设出拦截点的坐标,根据 ![]() ,用两点间距离公式分别表示PA、PB可得一个圆,然后比较点B到边界的距离与半径的大小。
,用两点间距离公式分别表示PA、PB可得一个圆,然后比较点B到边界的距离与半径的大小。


科目:高中数学 来源: 题型:
【题目】我国古代数学典籍《九章算术》“盈不足”中有一道问题:“今有垣高九尺,瓜生其上,蔓日长七寸;瓠生其下,蔓日长一尺,问几何日相逢?”现用程序框图描述,如图所示,则输出的结果n=( ) 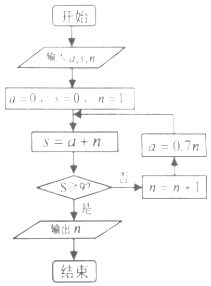
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆E: ![]() ,点P(0,1)在短轴CD上,且
,点P(0,1)在短轴CD上,且 ![]()
(Ⅰ) 求椭圆E的方程及离心率;
(Ⅱ) 设O为坐标原点,过点P的动直线与椭圆交于A,B两点.是否存在常数λ,使得 ![]() 为定值?若存在,求λ的值;若不存在,请说明理由.
为定值?若存在,求λ的值;若不存在,请说明理由.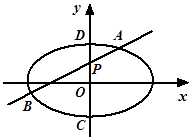
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,则(写出所有正确结论编号) ①四面体ABCD每组对棱相互垂直
②四面体ABCD每个面的面积相等
③从四面体ABCD每个顶点出发的三条棱两两夹角之和大于90°而小于180°
④连接四面体ABCD每组对棱中点的线段互垂直平分
⑤从四面体ABCD每个顶点出发的三条棱的长可作为一个三角形的三边长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() .有序数组
.有序数组 ![]() 经m次变换后得到数组
经m次变换后得到数组 ![]() ,其中
,其中 ![]() ,
, ![]() (
( ![]() 1,2,
1,2, ![]() ,n),
,n), ![]() ,
, ![]()
![]() .
.
例如:有序数组 ![]() 经1次变换后得到数组
经1次变换后得到数组 ![]() ,即
,即 ![]() ;经第2次变换后得到数组
;经第2次变换后得到数组 ![]() .
.
(1)若 ![]() ,求
,求 ![]() 的值;
的值;
(2)求证: ![]() ,其中
,其中 ![]() 1,2,
1,2, ![]() ,n.(注:当
,n.(注:当 ![]() 时,
时, ![]() ,
, ![]() 1,2,
1,2, ![]() ,n,则
,n,则 ![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,四边形ABCD为直角梯形,AD∥BC,AD⊥AB,AD=1,BC=2,E为CD上一点,F为BE的中点,且DE=1,EC=2,现将梯形沿BE折叠(如图2),使平面BCE⊥ABED.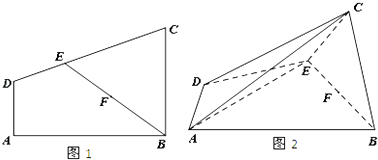
(1)求证:平面ACE⊥平面BCE;
(2)能否在边AB上找到一点P(端点除外)使平面ACE与平面PCF所成角的余弦值为 ![]() ?若存在,试确定点P的位置,若不存在,请说明理由.
?若存在,试确定点P的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于任意实数a,b,定义min{a,b}= ![]() ,定义在R上的偶函数f (x)满足f (x+4)=f(x),且当0≤x≤2时,f (x)=min{2x﹣1,2﹣x},若方程f (x)﹣mx=0恰有两个根,则m的取值范围是( )
,定义在R上的偶函数f (x)满足f (x+4)=f(x),且当0≤x≤2时,f (x)=min{2x﹣1,2﹣x},若方程f (x)﹣mx=0恰有两个根,则m的取值范围是( )
A.{﹣1,1}∪(﹣ln2,- ![]() )∪(
)∪( ![]() ,ln2)
,ln2)
B.[﹣1,- ![]() )∪
)∪ ![]()
C.{﹣1,1}∪(﹣ln2,- ![]() )∪(
)∪( ![]() ,ln2)
,ln2)
D.(- ![]() ,-
,- ![]() )∪(
)∪( ![]() ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com