
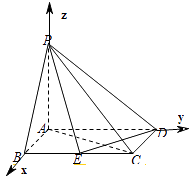
【题目】如图四棱锥P﹣ABCD底面是矩形,PA⊥平面ABCD,PA=AB=1, ![]() ,E是BC上的点,
,E是BC上的点, 
(1)试确定E点的位置使平面PED⊥平面PAC,并证明你的结论;
(2)在条件(1)下,求二面角B﹣PE﹣D的余弦值.
【答案】
(1)证明:以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
∵PA⊥平面ABCD,∴PA⊥DE,
若平面PED⊥平面PAC,
则需要ED⊥平面PAC,
即ED⊥AC即可.
∵PA=AB=1, ![]() ,
,
∴P(0,0,1),D(0, ![]() ,0),B(1,0,0),
,0),B(1,0,0),
C(1, ![]() ,0),
,0),
设BE=a,则E(1,a,0),
则 ![]() =(1,
=(1, ![]() ,0),
,0), ![]() =(﹣1,
=(﹣1, ![]() ﹣a,0),
﹣a,0),
由 ![]()
![]() =(1,
=(1, ![]() ,0)(﹣1,
,0)(﹣1, ![]() ﹣a,0)=0,
﹣a,0)=0,
得﹣1+ ![]() (
( ![]() ﹣a)=0,得a=
﹣a)=0,得a= ![]() ,即E是BC的中点.
,即E是BC的中点.
(2)解:在条件(1)下,即E是BC的中点,则E(1, ![]() ,0),
,0),
则 ![]() =(1,
=(1, ![]() ,﹣1),
,﹣1), ![]() =(0,
=(0, ![]() ,0),
,0), ![]() =(﹣1,
=(﹣1, ![]() ,0),
,0),
设平面BPE的法向量 ![]() =(x,y,z),平面PED的法向量
=(x,y,z),平面PED的法向量 ![]() =(x,y,z),
=(x,y,z),
则由 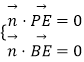 得
得 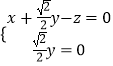 ,即
,即 ![]() ,令x=1,则z=1,即
,令x=1,则z=1,即 ![]() =(1,0,1),
=(1,0,1),
则由 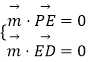 得
得 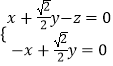 ,令y=
,令y= ![]() ,则x=1,z=2即
,则x=1,z=2即 ![]() =(1,
=(1, ![]() ,2),
,2),
则cos< ![]() ,
, ![]() >|=
>|= ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∵二面角B﹣PE﹣D是钝二面角,
∴二面角B﹣PE﹣D的余弦值为﹣ ![]() .
.
【解析】(1)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,利用向量法能证明ED⊥AC即可.(2)求出平面的法向量利用向量法即可求二面角B﹣PE﹣D的余弦值.
【考点精析】通过灵活运用平面与平面垂直的性质,掌握两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直即可以解答此题.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且λSn=λ﹣an , 其中λ≠0且λ≠﹣1.
(1)证明:{an}是等比数列,并求其通项公式;
(2)若 ![]() ,求λ.
,求λ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人上午7时,乘摩托艇以匀速vkm/h(8≤v≤40)从A港出发到距100km的B港去,然后乘汽车以匀速wkm/h(30≤w≤100)自B港向距300km的C市驶去.应该在同一天下午4至9点到达C市. 设乘坐汽车、摩托艇去目的地所需要的时间分别是xh,yh.
(1)作图表示满足上述条件的x,y范围;
(2)如果已知所需的经费p=100+3(5﹣x)+2(8﹣y)(元),那么v,w分别是多少时p最小?此时需花费多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣ax﹣1(a∈R).
(1)若对任意实数x,f(x)<0恒成立,求实数a的取值范围;
(2)当a>0时,解关于x的不等式f(x)<2x﹣3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R.当x<0时,f(x)=x3﹣1;当﹣1≤x≤1时,f(﹣x)=﹣f(x);当x> ![]() 时,f(x+
时,f(x+ ![]() )=f(x﹣
)=f(x﹣ ![]() ).则f(6)=( )
).则f(6)=( )
A.﹣2
B.﹣1
C.0
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,且此函数图象过点(1,5).
,且此函数图象过点(1,5).
(1)求实数m的值;
(2)判断f(x)奇偶性;
(3)讨论函数f(x)在[2,+∞)上的单调性?并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}满足a1=1,an+an+1=( ![]() )n(n∈N*),Sn=a1+4a2+42a3+…+4n﹣1an , 则5Sn﹣4nan=( )
)n(n∈N*),Sn=a1+4a2+42a3+…+4n﹣1an , 则5Sn﹣4nan=( )
A.n﹣1
B.n
C.2n
D.n2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1)所示,在直角梯形ABCD中, ![]() ,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图(2)所示.
,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图(2)所示. 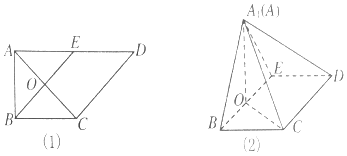
(1)证明:CD⊥平面A1OC;
(2)若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com