
【题目】已知集合M={(x,y)|x+y﹣2≤0,x≥0,y≥0},集合N={ ![]() },若点P∈M,则P∈M∩N的概率为( )
},若点P∈M,则P∈M∩N的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知曲线C在直角坐标系xOy下的参数方程为 ![]() (θ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(θ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)直线l的极坐标方程是ρcos(θ﹣ ![]() )=3
)=3 ![]() ,射线OT:θ=
,射线OT:θ= ![]() (ρ>0)与曲线C交于A点,与直线l交于B,求线段AB的长.
(ρ>0)与曲线C交于A点,与直线l交于B,求线段AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a为实常数,y=f(x)是定义在R上的奇函数,当x>0时,f(x)=4x+![]() +3,则对于y=f(x)在x<0时,下列说法正确的是( )
+3,则对于y=f(x)在x<0时,下列说法正确的是( )
A.有最大值7
B.有最大值﹣7
C.有最小值7
D.有最小值﹣7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称y=f(x)具有T性质.下列函数中具有T性质的是( )
A.y=sinx
B.y=lnx
C.y=ex
D.y=x3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲厂根据以往的生产销售经验得到下面有关生产销售的关系:厂里的固定成本为2.8万元,每生产1百台的生产成本为1万元,每生产产品x(百台),其总成本为G(x)(万元)(总成本=固定成本+生产成本).如果销售收入R(x)= ![]() ,且该产品产销平衡(即生产的产品都能卖掉),请完成下列问题:
,且该产品产销平衡(即生产的产品都能卖掉),请完成下列问题:
(1)写出利润函数y=f(x)的解析式(利润=销售收入﹣总成本);
(2)甲厂生产多少台新产品时,可使盈利最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图四棱锥P﹣ABCD底面是矩形,PA⊥平面ABCD,PA=AB=1, ![]() ,E是BC上的点,
,E是BC上的点, 
(1)试确定E点的位置使平面PED⊥平面PAC,并证明你的结论;
(2)在条件(1)下,求二面角B﹣PE﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(2x+1)定义域是[﹣1,0],则y=f(x+1)的定义域是( )
A.[﹣1,1]
B.[0,2]
C.[﹣2,0]
D.[﹣2,2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B,P在单位圆上,且B(﹣ ![]() ,
, ![]() ),∠AOB=α.
),∠AOB=α. 
(1)求 ![]() 的值;
的值;
(2)若四边形OAQP是平行四边形,
(i)当P在单位圆上运动时,求点O的轨迹方程;
(ii)设∠POA=θ(0≤θ≤2π),点Q(m,n),且f(θ)=m+ ![]() n.求关于θ的函数f(θ)的解析式,并求其单调增区间.
n.求关于θ的函数f(θ)的解析式,并求其单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则剩余部分体积与原四棱锥体积的比值为( )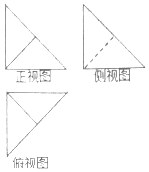
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com