
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为 ![]() (θ为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ=﹣2.
(θ为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ=﹣2.
(Ⅰ)求C1和C2在直角坐标系下的普通方程;
(Ⅱ)已知直线l:y=x和曲线C1交于M,N两点,求弦MN中点的极坐标.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,且此函数图象过点(1,5).
,且此函数图象过点(1,5).
(1)求实数m的值;
(2)判断f(x)奇偶性;
(3)讨论函数f(x)在[2,+∞)上的单调性?并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1)所示,在直角梯形ABCD中, ![]() ,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图(2)所示.
,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图(2)所示. 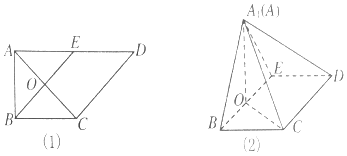
(1)证明:CD⊥平面A1OC;
(2)若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=f(x)导函数的图象如图所示,则下列说法错误的是( )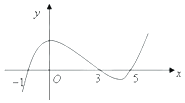
A.(﹣1,3)为函数y=f(x)的递增区间
B.(3,5)为函数y=f(x)的递减区间
C.函数y=f(x)在x=0处取得极大值
D.函数y=f(x)在x=5处取得极小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知U=R,M={x|﹣l≤x≤2},N={x|x≤3},则(UM)∩N=( )
A.{x|2≤x≤3}
B.{x|2<x≤3}
C.{x|x≤﹣1,或2≤x≤3}
D.{x|x<﹣1,或2<x≤3}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若a1=1,对任意的n∈N* , 都有an>0,且nan+12﹣(2n﹣1)an+1an﹣2an2=0设M(x)表示整数x的个位数字,则M(a2017)= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com