
【题目】已知数列{an}满足a1=4,an+1=qan+d(q,d为常数).
(1)当q=1,d=2时,求a2017的值;
(2)当q=3,d=﹣2时,记 ![]() ,Sn=b1+b2+b3+…+bn , 证明:
,Sn=b1+b2+b3+…+bn , 证明: ![]() .
.
【答案】
(1)解:∵数列{an}满足a1=4,an+1=qan+d(q,d为常数).
∴当q=1,d=2时,an+1﹣an=2,
∴数列{an}是首项a1=4,公差d=2的等差数列,
∴an=4+(n﹣1)×2=2n+2,
∴a2017=2×2017+2=4036
(2)证明:当q=3,d=﹣2时,an+1=3an﹣2变形得an+1﹣1=3(an﹣1)
∴数列{an﹣1}是以3为首项,3为公比的等比数列,
∴ ![]() ,∴
,∴ ![]() ,
,
∴数列{bn}是以 ![]() 为首项,
为首项, ![]() 为公比的等比数列,
为公比的等比数列,
∴ 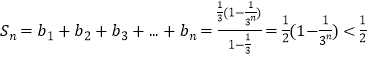 ,
,
∴ ![]()
【解析】(1)当q=1,d=2时,an+1﹣an=2,从而数列{an}是首项a1=4,公差d=2的等差数列,由此能求出a2017 . (2)当q=3,d=﹣2时,an+1=3an﹣2变形得an+1﹣1=3(an﹣1),从而数列{an﹣1}是以3为首项,3为公比的等比数列,进而数列{bn}是以 ![]() 为首项,
为首项, ![]() 为公比的等比数列,由此能证明
为公比的等比数列,由此能证明 ![]() .
.
【考点精析】根据题目的已知条件,利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系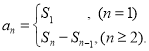 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}是公差不为0的等差数列,数列{bn}是等比数列,且b1=a1=1,b2=a3 , b3=a9
(1)求数列{an}的通项公式;
(2)求数列{anbn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边长分别为a,b,c,且cos ![]() =
= ![]() .
.
(1)若a=3,b= ![]() ,求c的值;
,求c的值;
(2)若f(A)=sin ![]() (
( ![]() cos
cos ![]() ﹣sin
﹣sin ![]() )+
)+ ![]() ,求f(A)的取值范围.
,求f(A)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}中,a1=1,an﹣an+1=anan+1 , n∈N* .
(1)求数列{an}的通项公式;
(2)Sn为{an}的前n项和,bn=S2n﹣Sn , 求bn的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学典籍《九章算术》“盈不足”中有一道问题:“今有垣高九尺,瓜生其上,蔓日长七寸;瓠生其下,蔓日长一尺,问几何日相逢?”现用程序框图描述,如图所示,则输出的结果n=( ) 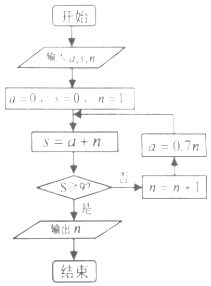
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】极坐标系与直角坐标系xOy取相同的长度单位,以原点O为极点,以x轴正半轴为极轴.已知直线l的参数方程为 ![]() 为参数).曲线C的极坐标方程为
为参数).曲线C的极坐标方程为 ![]() .
.
(1)求直线l的倾斜角和曲线C的直角坐标方程;
(2)设直线C与曲线C交于A,B两点,与x轴的交点为M,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两定点F1(﹣ ![]() ,0),F2(
,0),F2( ![]() ,0),满足条件|PF2|﹣|PF1|=2的点P的轨迹是曲线E.
,0),满足条件|PF2|﹣|PF1|=2的点P的轨迹是曲线E.
(1)求曲线E的方程;
(2)设过点(0,﹣1)的直线与曲线E交于A,B两点.如果|AB|=6 ![]() ,求直线AB的方程.
,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() sinxcosx﹣sin2x,把f(x)的图象向右平移
sinxcosx﹣sin2x,把f(x)的图象向右平移 ![]() 个单位,再向上平移2个单位,得到y=g(x)的图象,若对任意实数x,都有g(α﹣x)=g(α+x)成立,则g(α+
个单位,再向上平移2个单位,得到y=g(x)的图象,若对任意实数x,都有g(α﹣x)=g(α+x)成立,则g(α+ ![]() )+g(
)+g( ![]() )=( )
)=( )
A.4
B.3
C.2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() .有序数组
.有序数组 ![]() 经m次变换后得到数组
经m次变换后得到数组 ![]() ,其中
,其中 ![]() ,
, ![]() (
( ![]() 1,2,
1,2, ![]() ,n),
,n), ![]() ,
, ![]()
![]() .
.
例如:有序数组 ![]() 经1次变换后得到数组
经1次变换后得到数组 ![]() ,即
,即 ![]() ;经第2次变换后得到数组
;经第2次变换后得到数组 ![]() .
.
(1)若 ![]() ,求
,求 ![]() 的值;
的值;
(2)求证: ![]() ,其中
,其中 ![]() 1,2,
1,2, ![]() ,n.(注:当
,n.(注:当 ![]() 时,
时, ![]() ,
, ![]() 1,2,
1,2, ![]() ,n,则
,n,则 ![]() .)
.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com