
【题目】已知两定点F1(﹣ ![]() ,0),F2(
,0),F2( ![]() ,0),满足条件|PF2|﹣|PF1|=2的点P的轨迹是曲线E.
,0),满足条件|PF2|﹣|PF1|=2的点P的轨迹是曲线E.
(1)求曲线E的方程;
(2)设过点(0,﹣1)的直线与曲线E交于A,B两点.如果|AB|=6 ![]() ,求直线AB的方程.
,求直线AB的方程.
【答案】
(1)解:由双曲线的定义可知,曲线E是以F1(﹣ ![]() ,0),F2(
,0),F2( ![]() ,0)为焦点的双曲线的左支,且c=
,0)为焦点的双曲线的左支,且c= ![]() ,a=1,
,a=1,
∴b= ![]() =1,故曲线E的方程为x2﹣y2=1(x<0)
=1,故曲线E的方程为x2﹣y2=1(x<0)
(2)解:设A(x1,y1),B(x2,y2),由题意建立方程组 ![]() ,消去y,得(1﹣k2)x2+2kx﹣2=0,
,消去y,得(1﹣k2)x2+2kx﹣2=0,
又已知直线与双曲线左支交于两点A,B,有 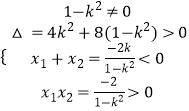 ,
,
解得﹣ ![]() <k<﹣1.
<k<﹣1.
∵|AB|= ![]() =
= ![]() =2
=2 ![]() =
= ![]() ,
,
∴28k4﹣55k2+25=0,
∴ ![]() 或
或 ![]() ,
,
∵﹣ ![]() <k<﹣1,
<k<﹣1,
∴ ![]() ,
,
∴直线AB的方程为 ![]()
【解析】(1)根据条件|PF2|﹣|PF1|=2,利用双曲线的定义,可求曲线E的方程;(2)直线方程代入双曲线方程,利用直线与双曲线左支交于两点A,B,求出k的范围,再利用|AB|=6 ![]() ,求出k的值,从而可求直线AB的方程.
,求出k的值,从而可求直线AB的方程.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4x+a2x+3,a∈R
(1)当a=﹣4时,且x∈[0,2],求函数f(x)的值域;
(2)若f(x)>0在(0,+∞)对任意的实数x恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=4,an+1=qan+d(q,d为常数).
(1)当q=1,d=2时,求a2017的值;
(2)当q=3,d=﹣2时,记 ![]() ,Sn=b1+b2+b3+…+bn , 证明:
,Sn=b1+b2+b3+…+bn , 证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《张丘建算经》是我国南北朝时期的一部重要数学著作,书中系统的介绍了等差数列,同类结果在三百多年后的印度才首次出现.书中有这样一个问题,大意为:某女子善于织布,后一天比前一天织的快,而且每天增加的数量相同,已知第一天织布5尺,一个月(按30天计算)总共织布390尺,问每天增加的数量为多少尺?该问题的答案为( )
A.![]() 尺
尺
B.![]() 尺
尺
C.![]() 尺
尺
D.![]() 尺
尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,点P在线段AD1上运动,则异面直线CP与BA1所成的角θ的取值范围是( )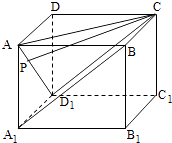
A.0<θ< ![]()
B.0<θ≤ ![]()
C.0≤θ≤ ![]()
D.0<θ≤ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l: 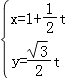 (t为参数),曲线C1:
(t为参数),曲线C1: ![]() (θ为参数).
(θ为参数).
(Ⅰ)设l与C1相交于A,B两点,求|AB|;
(Ⅱ)若把曲线C1上各点的横坐标压缩为原来的 ![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的 ![]() 倍,得到曲线C2 , 设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.
倍,得到曲线C2 , 设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高三年级随机抽取一个班,对该班50名学生的高校招生体检表中的视力情况进行统计,其频率分布直方图如图所示.若某高校A专业对视力的要求在0.9以上,则该班学生中能报A专业的人数为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等比数列,且a2013+a2015= ![]() dx,则a2014(a2012+2a2014+a2016)的值为( )
dx,则a2014(a2012+2a2014+a2016)的值为( )
A.π2
B.2π
C.π
D.4π2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com