
(本小题满分12分)一个容量为M的样本数据,其频率分布表如下.
(Ⅰ)表中a= ,b = ;
(Ⅱ)画出频率分布直方图;
(Ⅲ)用频率分布直方图,求出总体的众数及平均数的估计值.
频率分布表
| 分组 | 频数 | 频率 | 频率/组距 |
| (10,20] | 2 | 0.10 | 0.010 |
| (20,30] | 3 | 0.15 | 0.015 |
| (30,40] | 4 | 0.20 | 0.020 |
| (40,50] | a | b | 0.025 |
| (50,60] | 4 | 0.20 | 0.020 |
| (60, 70] | 2 | 0.10 | 0.010 |
(Ⅰ)a=5,b =0.25,
(Ⅱ)频率分布直方图,如图右所示: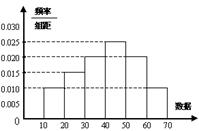
(Ⅲ)众数为: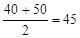 ,
,
平均数: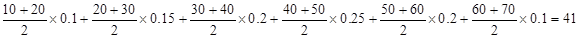
解析试题分析:(1)由于样本容量,频率和频数的关系得到结论。
(2)依照频率分布直方图和频率的概念得到。.
(3)结合直方图来表示众数和平均数的求解运用
(Ⅰ)a=5,b =0.25---------------------2分
(Ⅱ)频率分布直方图,如图右所示: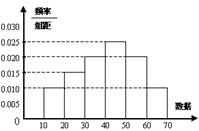 -------6分
-------6分
(Ⅲ)众数为: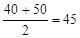 -----------------8分
-----------------8分
平均数: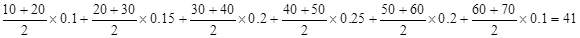 -------------------------------12分
-------------------------------12分
考点:本题主要考查了频率分布直方图的相关知识,以及频率=频数:样本容量,利用样本估计总体等有关知识,属于基础题.
点评:解决该试题的关键是能利用直方图来表格数据表述出各个组中 的频率以及频数,进而作图,确定出数字的特征。


科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如下(阴影部分为损坏数据),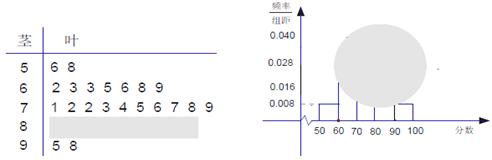
据此解答如下问题:
(1) 求本次测试成绩的中位数,并求频率分布直方图中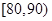 的矩形的高(用小数表示);
的矩形的高(用小数表示);
(2) 若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(11分)为了调查某厂2000名工人生产某种产品的能力,随机抽查了 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为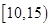 ,
,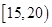 ,
,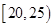 ,
,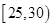 ,
,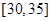 ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在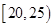 之间的工人有6位.
之间的工人有6位.
(Ⅰ)求 ;
;
(Ⅱ)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,则这2位工人不在同一组的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)某市调研考试后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的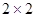 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为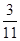 .
.
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合计 | | | 110 |
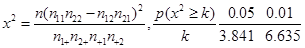 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2
表1:
| 生产能力分组 | 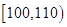 | 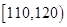 | 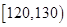 | 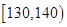 | 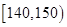 |
| 人数 | 4 | 8 |  | 5 | 3 |
| 生产能力分组 | 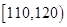 | 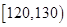 | 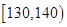 | 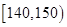 |
| 人数 | 6 | y | 36 | 18 |
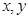 ,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)(注意:本题请在答题卡上作图)
,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)(注意:本题请在答题卡上作图)
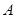 类工人和
类工人和 类工人生产能力的众数、中位数和平均数。(精确到0.1)
类工人生产能力的众数、中位数和平均数。(精确到0.1)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下表是关于某设备的使用年限(年)和所需要的维修费用y (万元)的几组统计数据:
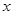 | 2 | 3 | 4 | 5 | 6 |
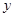 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
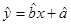 ;
;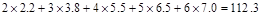 )
)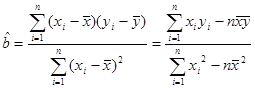 ;
;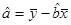 ;
; 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某班50位学生期中考试数学成绩的频率分布直方图如图所示,成绩分组区间是:[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
(Ⅰ)求图中 x的值;
(Ⅱ)从成绩不低于80分的学生中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)
随机调查某社区80个人,以研究这一社区居民在20:00-22:00时间段的休闲方式与性别有关系,得到下面的数据表:
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 10 | 50 | 60 |
| 女 | 10 | 10 | 20 |
| 合计 | 20 | 60 | 80 |
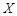 ,求
,求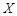 的分布列和期望;
的分布列和期望;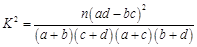 ,其中
,其中
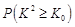 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
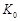 | 2.072 | 2.706 | 3.841 | 5.042 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某网站欲调查网民对当前网页的满意程度,在登录的所有网民中,收回有效帖子
50000份,其中持各种态度的份数如下表所示.
很满 意 意 | 满意 | 一般 | 不满意 |
| 10800 | 12400 | 15600 | 11200 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com