
某网站欲调查网民对当前网页的满意程度,在登录的所有网民中,收回有效帖子
50000份,其中持各种态度的份数如下表所示.
很满 意 意 | 满意 | 一般 | 不满意 |
| 10800 | 12400 | 15600 | 11200 |
科目:高中数学 来源: 题型:解答题
(本小题满分12分)一个容量为M的样本数据,其频率分布表如下.
(Ⅰ)表中a= ,b = ;
(Ⅱ)画出频率分布直方图;
(Ⅲ)用频率分布直方图,求出总体的众数及平均数的估计值.
频率分布表
| 分组 | 频数 | 频率 | 频率/组距 |
| (10,20] | 2 | 0.10 | 0.010 |
| (20,30] | 3 | 0.15 | 0.015 |
| (30,40] | 4 | 0.20 | 0.020 |
| (40,50] | a | b | 0.025 |
| (50,60] | 4 | 0.20 | 0.020 |
| (60, 70] | 2 | 0.10 | 0.010 |
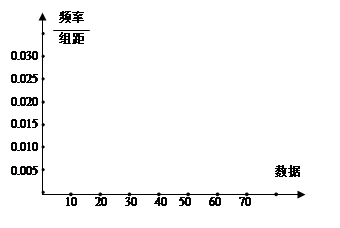
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组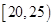 ,第2组
,第2组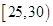 ,第3组
,第3组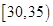 ,第4组
,第4组 ,第5组
,第5组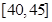 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.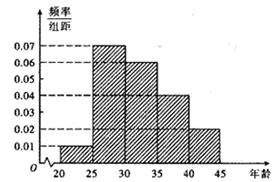
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)某班同学利用暑期进行社会实践,对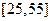 岁的人群随机抽取
岁的人群随机抽取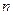 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图: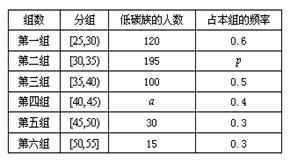
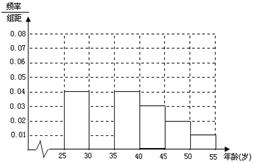
(Ⅰ)补全频率分布直方图并求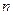 、
、 、
、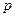 的值;
的值;
(Ⅱ)从年龄段在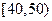 的“低碳族”中采用分层抽样法抽取
的“低碳族”中采用分层抽样法抽取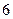 人参加户外低碳体验活动,其中选取
人参加户外低碳体验活动,其中选取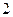 人作为领队,求选取的
人作为领队,求选取的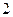 名领队中恰有1人年龄在
名领队中恰有1人年龄在 岁的概率。
岁的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
调查在2~3级风时的海上航行中男女乘客的晕船情况,共调查了71人,其中女性34人,男性37人。女性中有10人晕船,另外24人不晕船;男性中有12人晕船,另外25人不晕船。
判断晕船是否与性别有关系。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
由世界自然基金会发起的“地球1小时”活动,已发展成为最有影响力的环保活动之一,今年的参与人数再创新高.然而也有部分公众对该活动的实际效果与负面影响提出了疑问.对此,某新闻媒体进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
| | 支持 | 保留 | 不支持 |
| 20岁以下 | 800 | 450 | 200 |
| 20岁以上(含20岁) | 100 | 150 | 300 |
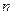 个人,已知从“支持”态度的人中抽取了45人,求
个人,已知从“支持”态度的人中抽取了45人,求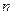 的值;
的值;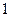 人20岁以下的概率;
人20岁以下的概率;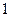 个数,求该数与总体平均数之差的绝对值超过0.6的概率.
个数,求该数与总体平均数之差的绝对值超过0.6的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂对某产品的产量与单位成本的资料分析后有如下数据:
| 月 份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 产量x千件 | 2 | 3 | 4 | 3 | 4 | 5 |
| 单位成本y元/件 | 73 | 72 | 71 | 73 | 69 | 68 |
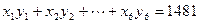 ,结果保留两位小数)
,结果保留两位小数)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段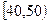 ,
,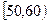 …
…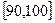 后画出如下频率
后画出如下频率 分布直方图.观察图形的信息,回答下列问题:
分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)估计这次考试的众数m与中位数n(结果保留一位小数);
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分.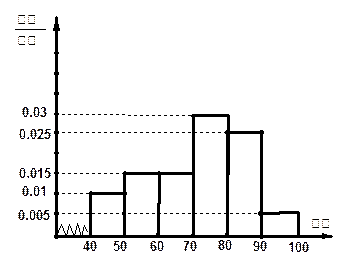
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某中学研究性学习小组,为了考察高中学生的作文水平与爱看课外书的关系,在本校高三年级随机调查了 50名学生.调査结果表明:在爱看课外书的25人中有18人作文水平好,另7人作文水平一般;在不爱看课外书的25人中有6人作文水平好,另19人作文水平一般.
(Ⅰ)试根据以上数据完成以下2×2列联表,并运用独 立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
高中学生的作文水平与爱看课外书的2×2列联表
| | 爱看课外书 | 不爱看课外书 | 总计 |
作文水平 好 好 | | | |
| 作文水平一般 | [来源:学。科。网Z。X。X。K] | | |
| 总计 | | | |
 分别编号为1、2、3、4、5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
分别编号为1、2、3、4、5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.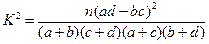 ,其中
,其中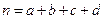 .
.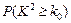 [来源:学*科*网] [来源:学*科*网] | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
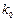 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com