
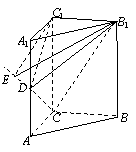
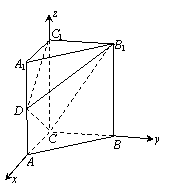
(08年黄冈中学三模)如图,在直三棱柱ABC―A1B1C1中, ![]() .
.
(Ⅰ)若D为AA1中点,求证:平面B1CD![]() 平面B1C1D;
平面B1C1D;
(Ⅱ)若二面角B1―DC―C1的大小为60°,求AD的长.

解析:解法一:(Ⅰ)∵![]() ,∴
,∴![]() ,
,
又由直三棱柱性质知![]() ,∴
,∴![]() 平面ACC1A1.
平面ACC1A1.
∴![]() ……①
……①
由D为中点可知,![]() ,∴
,∴![]()
即![]() ……②
……②
由①②可知![]() 平面B1C1D,又
平面B1C1D,又![]() 平面B1CD,
平面B1CD,
故平面![]() 平面B1C1D.
平面B1C1D.
(Ⅱ)由(1)可知![]() 平面ACC1A1,如图,
平面ACC1A1,如图,
在面ACC1A1内过C1作![]() ,
,
交CD或延长线或于E,连EB1,
由三垂线定理可知![]() 为二面角B1―DC―C1的平面角,
为二面角B1―DC―C1的平面角,
∴![]()
由B1C1=2知,![]() ,设AD=x,则
,设AD=x,则![]()
∵![]() 的面积为1,
的面积为1,
∴![]() ,解得
,解得![]() ,即
,即![]()
解法二:(Ⅰ)如图,以C为原点,CA、CB、CC1所在直线为x, y, z轴建立空间直角坐标系.
则 C(0,0,0),A(1,0,0),B1(0,2,2),C1(0,0,2),D(1,0,1).
即![]()
由![]() ,得
,得![]() ;
;
由![]() ,得
,得![]() ;
;
又![]() ,∴
,∴![]() 平面B1C1D.
平面B1C1D.
又![]() 平面B1CD,
平面B1CD,
∴平面![]() 平面B1C1D.
平面B1C1D.
(Ⅱ)设AD=a,则D点坐标为(1,0,a),![]() ,
,
设平面B1CD的法向量为![]() . 则由
. 则由![]() ,令z= -1,
,令z= -1,
得![]() ,又平面C1DC的法向量为
,又平面C1DC的法向量为![]() ,则由
,则由![]() ,即
,即![]() ,故
,故![]()


科目:高中数学 来源: 题型:
(08年黄冈中学三模理)设![]() 的极小值为
的极小值为![]() ,其导函数
,其导函数![]() 的图像是经过点
的图像是经过点![]() 开口向上的抛物线,如图所示.
开口向上的抛物线,如图所示.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)若直线![]() 与函数
与函数![]() 有三个交点,
有三个交点,
求实数![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
(08年黄冈中学三模理)如图,设抛物线![]()
![]() 的准线与
的准线与![]() 轴交于
轴交于![]() ,焦点为
,焦点为![]() ;以
;以![]() 为焦点,离心率
为焦点,离心率![]() 的椭圆
的椭圆![]() 与抛物线
与抛物线![]() 在
在![]() 轴上方的一个交点为
轴上方的一个交点为![]() .
.
(Ⅰ)当![]() 时,求椭圆的方程及其右准线的方程;
时,求椭圆的方程及其右准线的方程;
(Ⅱ)在(Ⅰ)的条件下,直线![]() 经过椭圆
经过椭圆![]() 的右焦点
的右焦点![]() ,与抛物线
,与抛物线![]() 交于
交于![]() ,如果
,如果
以线段![]() 为直径作圆,试判断点P与圆的位置关系,并说明理由;
为直径作圆,试判断点P与圆的位置关系,并说明理由;
(Ⅲ)是否存在实数![]() ,使得△
,使得△![]() 的边长是连续的自然数,若存在,求出这样的实数
的边长是连续的自然数,若存在,求出这样的实数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
(08年黄冈中学三模文)(本小题满分13分)设![]() 的极小值为
的极小值为![]() ,其导函数
,其导函数![]() 的图像是经过点
的图像是经过点![]() 开口向上的抛物线,如图所示.
开口向上的抛物线,如图所示.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)若![]()
![]()
![]() ,且过点(1,m)可作曲线
,且过点(1,m)可作曲线![]() 的三条切线,求实数
的三条切线,求实数![]() 的取值范围.
的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com