
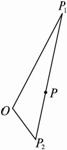
解:以O为原点,∠P1OP2的平分线为x轴建立直角坐标系,设双曲线的方程为![]() ,由于双曲线的离心率为
,由于双曲线的离心率为![]() ,∴e2=
,∴e2=![]() .?
.?
∴![]() .∴两条渐近线的方程为y=±
.∴两条渐近线的方程为y=±![]() x. ?
x. ?
由此设点P1(x1,![]() x1),P2(x2,-
x1),P2(x2,-![]() x2)(x1>0,x2>0),由题设知点P分P1P2所成的比λ=2,得点P的坐标为(
x2)(x1>0,x2>0),由题设知点P分P1P2所成的比λ=2,得点P的坐标为(![]() ,
,![]() ),又点P在双曲线上,?
),又点P在双曲线上,?
∴![]() -
-![]() =1,即(x1+2x2)2-(x1-2x2)2=
=1,即(x1+2x2)2-(x1-2x2)2=
又|OP1|=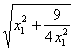 =
=![]() x1, |OP2|=
x1, |OP2|=![]() x2且sin∠P1OP2=
x2且sin∠P1OP2=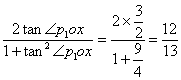 .
.
?
∴S△=![]() |OP1||OP2|sin∠P1OP2=
|OP1||OP2|sin∠P1OP2=![]() ×
×![]() x1x2×
x1x2×![]() =
=![]() ,由此得x1x2=
,由此得x1x2=![]() .代入①式得a2=4,?
.代入①式得a2=4,?
∴b2=9,所求方程为![]() .
.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源:2013-2014学年山西省高三上学期期中考试理科数学试卷(解析版) 题型:解答题
如图已知抛物线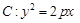 的焦点坐标为
的焦点坐标为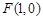 ,过
,过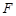 的直线交抛物线
的直线交抛物线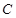 于
于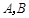 两点,直线
两点,直线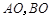 分别与直线
分别与直线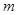 :
: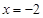 相交于
相交于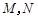 两点.
两点.
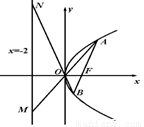
(1)求抛物线 的方程;
的方程;
(2)证明△ABO与△MNO的面积之比为定值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省广州市高三数学解析几何专题试卷 题型:解答题
(本小题满分14分)
如图已知△OPQ的面积为S,且 .
.
(Ⅰ)若 的取值范围;
的取值范围;
|
 为中心,P为焦点的椭圆经过点Q,当m≥2时,求
为中心,P为焦点的椭圆经过点Q,当m≥2时,求 的最小值,并求出此时的椭圆方程。
的最小值,并求出此时的椭圆方程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com