【题目】已知数列
的前
项和为
，且
（
）．
（1）求
的通项公式；
（2）设
， 
， 
是数列
的前
项和，求正整数
，使得对任意
均有
恒成立；
（3）设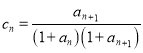
， 
是数列
的前
项和，若对任意
均有
恒成立，求
的最小值．
【答案】（1）
（2）
或5（3）
【解析】试题分析: (1)由
与
之间的关系求出
的通项公式; (2)先求出数列
的通项公式,方法一是求出
增减情况,正负情况,求出
的最大项,方法二是求出
的前n项和
，再求出
，得出
的增减性，再求出
的最大值; (3)用裂项相消法求出数列
的前n项和
， 
,再求出
的范围.
试题解析: 由
，得
两式相减，得
∴
数列
为等比数列，公比
又
，得
， 
∴ 
（2）
， 
方法一当
时， 
因此， 
∴ 对任意
均有
，故
或
。
方法二（
两式相减，得
=
，
，
当
，当
，当
时， 
，
综上，当且仅当
或5时，均有
（3）∵
∴ 
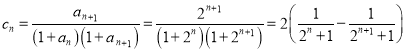
∵对任意
均有
成立，
∴
，
所以
的最小值为
点睛: 本题主要考查了数列有关问题,涉及的知识点有求数列通项公式,用裂项相消法求和,判断数列的增减性等,属于中档题.
科目：高中数学 来源： 题型：
【题目】如图，在等腰梯形
中， 
， 
， 
，四边形
为矩形， 
，平面
平面
，点
为线段
中点．
（Ⅰ）求异面直线
与
所成的角的正切值；
（Ⅱ）求证：平面
平面
；
（Ⅲ）求直线
与平面
所成角的正弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
.
（1）若椭圆
的右焦点坐标为
，求
的值；
（2）由椭圆
上不同三点构成三角形称为椭圆的内接三角形.若以
为直角顶点的椭圆
的内接等腰直角三角形恰有三个，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图是一个正方体的展开图，如果将它还原为正方体，那么NC、DE、AF、BM这四条线段所在的直线是异面直线的有多少对？试以其中一对为例进行证明．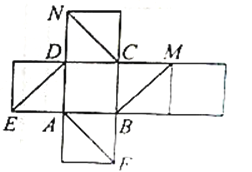
查看答案和解析>>
科目：高中数学 来源： 题型：
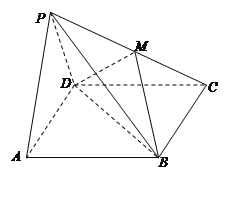
【题目】如图，在四棱锥
中，底面
是矩形，面
底面
，且
是边长为
的等边三角形， 
， 
在
上，且
∥面BDM.
（1）求直线PC与平面BDM所成角的正弦值；
（2）求平面BDM与平面PAD所成锐二面角的大小.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】函数f（x）=2ax2﹣2bx﹣a+b（a，b∈R，a＞0），g（x）=2ax﹣2b
（1）若
时，求f（sinθ）的最大值；
（2）设a＞0时，若对任意θ∈R，都有|f（sinθ）|≤1恒成立，且g（sinθ）的最大值为2，求f（x）的表达式．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
