
【题目】大学先修课程是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备.某高中成功开设大学先修课程已有两年,共有![]() 人参与学习先修课程,这两年学习先修课程的学生都参加了高校的自主招生考试(满分
人参与学习先修课程,这两年学习先修课程的学生都参加了高校的自主招生考试(满分![]() 分),结果如下表所示:
分),结果如下表所示:
分数 |
|
|
|
|
|
人数 |
|
|
|
|
|
参加自主招生获得通过的概率 |
|
|
|
|
|
(1)这两年学校共培养出优等生![]() 人,根据图中等高条形图,填写相应列联表,并根据列联表检验能否在犯错的概率不超过
人,根据图中等高条形图,填写相应列联表,并根据列联表检验能否在犯错的概率不超过![]() 的前提下认为学习先修课程与优等生有关系?
的前提下认为学习先修课程与优等生有关系?
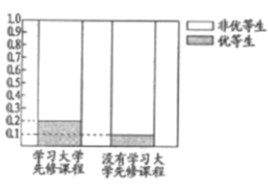
优等生 | 非优等生 | 总计 | |
学习大学先修课程 |
| ||
没有学习大学先修课程 | |||
总计 |
|
(2)已知今年全校有![]() 名学生报名学习大学选项课程,并都参加了高校的自主招生考试,以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
名学生报名学习大学选项课程,并都参加了高校的自主招生考试,以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
(i)在今年参与大学先修课程学习的学生中任取一人,求他获得高校自主招生通过的概率;
(ii)某班有![]() 名学生参加了大学先修课程的学习,设获得高校自主招生通过的人数为
名学生参加了大学先修课程的学习,设获得高校自主招生通过的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: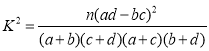 ,其中
,其中![]() .
.
【答案】(1)见解析,在犯错误的概率不超过![]() 的前提下认为学习先修课程与优等生有关系.(2)(i)
的前提下认为学习先修课程与优等生有关系.(2)(i)![]() (ii)见解析,
(ii)见解析,![]()
【解析】
(1)作出列联表,由列联表求出![]() .从而在犯错误的概率不超过0.01的前提下认为学习先修课程与优等生有关系.
.从而在犯错误的概率不超过0.01的前提下认为学习先修课程与优等生有关系.
(2)![]() 由题意利用互斥事件概率加法公式能求出他获得高校自主招生通过的概率.
由题意利用互斥事件概率加法公式能求出他获得高校自主招生通过的概率.
![]() 设获得高校自主招生通过的人数为
设获得高校自主招生通过的人数为![]() ,则
,则![]() ,由此能求出
,由此能求出![]() 的分布列,即可求出期望.
的分布列,即可求出期望.
解:(1)列联表如下:
优等生 | 非优等生 | 总计 | |
学习大学先修课程 |
|
|
|
没有学习大学先修课程 |
|
|
|
总计 |
|
|
|
由列联表可得![]() ,
,
因此在犯错误的概率不超过![]() 的前提下认为学习先修课程与优等生有关系.
的前提下认为学习先修课程与优等生有关系.
(2)(i)由题意得所求概率为![]() .
.
(ii)设获得高校自主招生通过的人数为![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】根据气象部门预报,在距离某个码头A南偏东45°方向的600km处的热带风暴中心B正以30km/h的速度向正北方向移动,距离风暴中心450km以内的地区都将受到影响,从现在起经过___小时后该码头A将受到热带风暴的影响(精确到0.01).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过
经过![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,且与圆
有且仅有一个公共点,且与圆![]() 相交于
相交于![]() 两点,试问直线
两点,试问直线![]() 与
与![]() 的斜率之积
的斜率之积![]() 是否为定值?若是,求出该定值;若不是,说明理由.
是否为定值?若是,求出该定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学德育处为了解全校学生的上网情况,在全校随机抽取了40名学生(其中男、女生人数各占一半)进行问卷调查,并进行了统计,按男、女分为两组,再将每组学生的月上网次数分为5组:![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
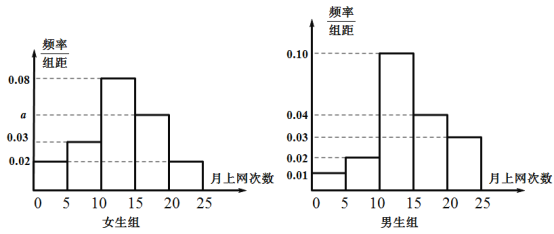
(1)写出女生组频率分布直方图中![]() 的值;
的值;
(2)求抽取的40名学生中月上网次数不少于15的学生人数;
(3)在抽取的40名学生中从月上网次数不少于20的学生中随机抽取3人,并用![]() 表示随机抽取的3人中男生的人数,求
表示随机抽取的3人中男生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱柱ABCD﹣A1B1C1D1中,∠BAD=∠BCD=90°,∠ADC=60°且AD=CD,BB1⊥平面ABCD,BB1=2AB=2.
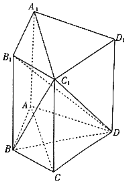
(1)证明:AC⊥B1D.
(2)求BC1与平面B1C1D所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种大型医疗检查机器生产商,对一次性购买2台机器的客户,推出两种超过质保期后两年内的延保维修优惠方案:方案一:交纳延保金7000元,在延保的两年内可免费维修2次,超过2次每次收取维修费2000元;方案二:交纳延保金10000元,在延保的两年内可免费维修4次,超过4次每次收取维修费1000元.某医院准备一次性购买2台这种机器。现需决策在购买机器时应购买哪种延保方案,为此搜集并整理了50台这种机器超过质保期后延保两年内维修的次数,得下表:
维修次数 | 0 | 1 | 2 | 3 |
台数 | 5 | 10 | 20 | 15 |
以这50台机器维修次数的频率代替1台机器维修次数发生的概率,记X表示这2台机器超过质保期后延保的两年内共需维修的次数。
(1)求X的分布列;
(2)以所需延保金及维修费用的期望值为决策依据,医院选择哪种延保方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了对某种商品进行合理定价,需了解该商品的月销售量![]() (单位:万件)与月销售单价
(单位:万件)与月销售单价![]() (单位:元/件)之间的关系,对近
(单位:元/件)之间的关系,对近![]() 个月的月销售量
个月的月销售量![]() 和月销售单价
和月销售单价![]()
![]() 数据进行了统计分析,得到一组检测数据如表所示:
数据进行了统计分析,得到一组检测数据如表所示:
月销售单价 |
|
|
|
|
|
|
月销售量 |
|
|
|
|
|
|
(1)若用线性回归模型拟合![]() 与
与![]() 之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:
之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:![]() ,
,![]() 和
和![]() ,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
(2)若用![]() 模型拟合
模型拟合![]() 与
与![]() 之间的关系,可得回归方程为
之间的关系,可得回归方程为![]() ,经计算该模型和(1)中正确的线性回归模型的相关指数
,经计算该模型和(1)中正确的线性回归模型的相关指数![]() 分别为
分别为![]() 和
和![]() ,请用
,请用![]() 说明哪个回归模型的拟合效果更好;
说明哪个回归模型的拟合效果更好;
(3)已知该商品的月销售额为![]() (单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到
(单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到![]() )
)
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大型中华传统文化电视节目《![]() 中国诗词大会》以“赏中华诗词,寻文化基因,品生活之美”为宗旨,深受广大观众喜爱,各基层单位也通过各种形式积极组织、选拔和推荐参赛选手.某单位制定规则如下:(1)凡报名参赛的诗词爱好者必须先后通过笔试和面试,方可获得入围
中国诗词大会》以“赏中华诗词,寻文化基因,品生活之美”为宗旨,深受广大观众喜爱,各基层单位也通过各种形式积极组织、选拔和推荐参赛选手.某单位制定规则如下:(1)凡报名参赛的诗词爱好者必须先后通过笔试和面试,方可获得入围![]() 正赛的推荐资格;(2)笔试成绩不低于85分的选手进入面试,面试成绩最高的3人获得推荐资格.在该单位最近组织的一次选拔活动中,随机抽取了一个笔试成绩的样本,据此绘制成频率分布直方图(如图
正赛的推荐资格;(2)笔试成绩不低于85分的选手进入面试,面试成绩最高的3人获得推荐资格.在该单位最近组织的一次选拔活动中,随机抽取了一个笔试成绩的样本,据此绘制成频率分布直方图(如图![]() .同时,也绘制了所有面试成绩的茎叶图(如图2,单位:分).
.同时,也绘制了所有面试成绩的茎叶图(如图2,单位:分).

(Ⅰ)估计该单位本次报名参赛的诗词爱好者的总人数;
(Ⅱ)若从面试成绩高于(不含)中位数的选手中随机选取3人,设其中获得推荐资格的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ).
).
(1)写出曲线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若射线![]() (
(![]() )与曲线
)与曲线![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() 两点(不是原点),求
两点(不是原点),求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com