
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ).
).
(1)写出曲线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若射线![]() (
(![]() )与曲线
)与曲线![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() 两点(不是原点),求
两点(不是原点),求![]() 的最大值.
的最大值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】大学先修课程是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备.某高中成功开设大学先修课程已有两年,共有![]() 人参与学习先修课程,这两年学习先修课程的学生都参加了高校的自主招生考试(满分
人参与学习先修课程,这两年学习先修课程的学生都参加了高校的自主招生考试(满分![]() 分),结果如下表所示:
分),结果如下表所示:
分数 |
|
|
|
|
|
人数 |
|
|
|
|
|
参加自主招生获得通过的概率 |
|
|
|
|
|
(1)这两年学校共培养出优等生![]() 人,根据图中等高条形图,填写相应列联表,并根据列联表检验能否在犯错的概率不超过
人,根据图中等高条形图,填写相应列联表,并根据列联表检验能否在犯错的概率不超过![]() 的前提下认为学习先修课程与优等生有关系?
的前提下认为学习先修课程与优等生有关系?
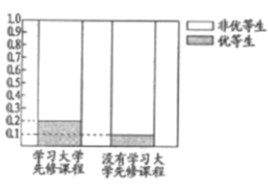
优等生 | 非优等生 | 总计 | |
学习大学先修课程 |
| ||
没有学习大学先修课程 | |||
总计 |
|
(2)已知今年全校有![]() 名学生报名学习大学选项课程,并都参加了高校的自主招生考试,以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
名学生报名学习大学选项课程,并都参加了高校的自主招生考试,以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
(i)在今年参与大学先修课程学习的学生中任取一人,求他获得高校自主招生通过的概率;
(ii)某班有![]() 名学生参加了大学先修课程的学习,设获得高校自主招生通过的人数为
名学生参加了大学先修课程的学习,设获得高校自主招生通过的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: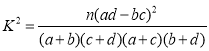 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有5个匣子,每个匣子有一把钥匙,并且钥匙不能通用.如果随意在每一个匣内放入一把钥匙,然后把匣子全都锁上.现在允许砸开一个匣子,使得能相继用钥匙打开其余4个匣子,那么钥匙的放法有______种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市工会组织了一次工人综合技能比赛,一共有![]() 名工人参加,他们的成绩都分布在
名工人参加,他们的成绩都分布在![]() 内,数据经过汇总整理得到如下的频率分布直方图,规定成绩在
内,数据经过汇总整理得到如下的频率分布直方图,规定成绩在![]() 分及
分及![]() 分以上的为优秀.
分以上的为优秀.

(1)求图中![]() 的值;
的值;
(2)估计这次比赛成绩的平均数(同一组中的数据以这组数据所在区间中点的值作代表);
(3)某工厂车间有![]() 名工人参加这次比赛,他们的成绩分布和整体的成绩分布情况完全一致,若从该车间参赛的且成绩为优秀的工人中任选两人,求这两人成绩均低于
名工人参加这次比赛,他们的成绩分布和整体的成绩分布情况完全一致,若从该车间参赛的且成绩为优秀的工人中任选两人,求这两人成绩均低于![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农业观光区的平面示意图如图所示,其中矩形![]() 的长
的长![]() 千米,宽
千米,宽![]() 千米,半圆的圆心
千米,半圆的圆心![]() 为
为![]() 中点,为了便于游客观光休闲,在观光区铺设一条由圆弧
中点,为了便于游客观光休闲,在观光区铺设一条由圆弧![]() 、线段
、线段![]() 、
、![]() 组成的观光道路,其中线段
组成的观光道路,其中线段![]() 经过圆心
经过圆心![]() ,点
,点![]() 在线段
在线段![]() 上(不含线段端点
上(不含线段端点![]() 、
、![]() ),已知道路
),已知道路![]() 、
、![]() 的造价为每千米
的造价为每千米![]() 万元,道路
万元,道路![]() 造价为每千米
造价为每千米![]() 万元,设
万元,设![]() ,观光道路的总造价为
,观光道路的总造价为![]() .
.
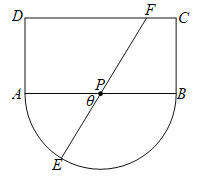
(1)试求![]() 与
与![]() 的函数关系式
的函数关系式![]() ,并写出
,并写出![]() 的取值范围;
的取值范围;
(2)当![]() 为何值时,观光道路的总造价
为何值时,观光道路的总造价![]() 最小.
最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点F到右准线的距离为3.
,右焦点F到右准线的距离为3.
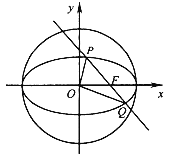
(1)求椭圆C的标准方程;
(2)设过F的直线l与椭圆C相交于P,Q两点.已知l被圆O:x2+y2=a2截得的弦长为![]() ,求△OPQ的面积.
,求△OPQ的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,![]() 为正三角形,且侧面PAB⊥底面ABCD,
为正三角形,且侧面PAB⊥底面ABCD, ![]() 为线段
为线段![]() 的中点,
的中点, ![]() 在线段
在线段![]() 上.
上.
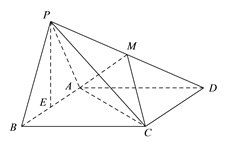
(I)当![]() 是线段
是线段![]() 的中点时,求证:PB // 平面ACM;
的中点时,求证:PB // 平面ACM;
(II)求证: ![]() ;
;
(III)是否存在点![]() ,使二面角
,使二面角![]() 的大小为60°,若存在,求出
的大小为60°,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com