
【题目】已知数列![]() 满足:
满足: ![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由![]() ;得
;得![]() ,两式相减可得结果;(2)由(1)可得
,两式相减可得结果;(2)由(1)可得![]() ,利用错位相减法求和即可.
,利用错位相减法求和即可.
试题解析:(1)当n=1时,a1=4-![]() =1.
=1.
当n≥2时,
a1+2a2+…+nan=4-![]() ..........................①
..........................①
a1+2a2+…+(n-1)an=4-![]() ..........................②
..........................②
①-②得: nan=![]() -
-![]() =
=![]() (2n+2-n-2)=
(2n+2-n-2)= ![]()
an=![]()
当n=1时,a1也适合上式, ∴an=![]() (nN*).
(nN*).
(2) bn=(3n-2) ![]()
Sn=![]() +
+![]() +
+![]() +…+(3n-5)
+…+(3n-5) ![]() +(3n-2)
+(3n-2)![]() ......................①
......................①
![]() Sn=
Sn=![]() +
+![]() +
+![]() +…+(3n-5)
+…+(3n-5) ![]() +(3n-2)
+(3n-2)![]() ......................②
......................②
①-②得: ![]() Sn=
Sn=![]() +3(
+3(![]() +
+![]() +
+![]() +…+
+…+![]() )-(3n-2)
)-(3n-2) ![]() =1+
=1+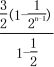 -(3n-2)
-(3n-2) ![]()
解得:Sn=8-![]() .
.
【 方法点睛】本题主要考查等比数列和等差数列的通项以及错位相减法求数列的通项,属于中档题.一般地,如果数列![]() 是等差数列,
是等差数列, ![]() 是等比数列,求数列
是等比数列,求数列![]() 的前
的前![]() 项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列
项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列![]() 的公比,然后作差求解, 在写出“
的公比,然后作差求解, 在写出“![]() ”与“
”与“![]() ” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“
” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“![]() ”的表达式.
”的表达式.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S. ①当 ![]() 时,S为四边形
时,S为四边形
②截面在底面上投影面积恒为定值 ![]()
③不存在某个位置,使得截面S与平面A1BD垂直
④当 ![]() 时,S与C1D1的交点满足C1R1=
时,S与C1D1的交点满足C1R1= ![]()
其中正确命题的个数为 ( )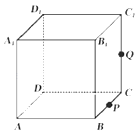
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的二次方程x2+2mx+2m+1=0.
(1)若方程有两个正根,求m的取值范围.
(2)若方程有两根,其中一根在区间(﹣1,0)内,另一根在区间(1,3)内,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于任意实数a,b,c,d,以下四个命题中的真命题是( )
A.若a>b,c≠0则ac>bc
B.若a>b>o,c>d则ac>bd
C.若a>b,则 ![]()
D.若ac2>bc2则a>b
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的两个焦点为![]() ,
, ![]() 是椭圆上一点,若
是椭圆上一点,若![]() ,
, ![]() .
.
(1)求椭圆的方程;
(2)直线![]() 过右焦点
过右焦点![]() (不与
(不与![]() 轴重合)且与椭圆相交于不同的两点
轴重合)且与椭圆相交于不同的两点![]() ,在
,在![]() 轴上是否存在一个定点
轴上是否存在一个定点![]() ,使得
,使得![]() 的值为定值?若存在,写出
的值为定值?若存在,写出![]() 点的坐标(不必求出定值);若不存在,说明理由.
点的坐标(不必求出定值);若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x﹣1.
(1)求f(3)+f(﹣1);
(2)求f(x)在R上的解析式;
(3)求不等式﹣7≤f(x)≤3的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 支篮球队进行单循环比赛(任两支球队恰进行一场比赛),任两支球队之间胜率都是
支篮球队进行单循环比赛(任两支球队恰进行一场比赛),任两支球队之间胜率都是![]() .单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题:
.单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题:
![]() :恰有四支球队并列第一名为不可能事件;
:恰有四支球队并列第一名为不可能事件; ![]() :有可能出现恰有两支球队并列第一名;
:有可能出现恰有两支球队并列第一名;
![]() :每支球队都既有胜又有败的概率为
:每支球队都既有胜又有败的概率为![]() ;
; ![]() :五支球队成绩并列第一名的概率为
:五支球队成绩并列第一名的概率为![]() .
.
其中真命题是
A. ![]() ,
,![]() ,
,![]() B.
B. ![]() ,
,![]() ,
,![]() C.
C. ![]() .
.![]() .
.![]() D.
D. ![]() .
.![]() .
.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 过点
过点![]() ,
, ![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() 的右、下顶点,且
的右、下顶点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 在椭圆
在椭圆![]() 内,满足直线
内,满足直线![]() ,
, ![]() 的斜率乘积为
的斜率乘积为![]() ,且直线
,且直线![]() ,
, ![]() 分别交椭圆
分别交椭圆![]() 于点
于点![]() ,
, ![]() .
.
(i) 若![]() ,
, ![]() 关于
关于![]() 轴对称,求直线
轴对称,求直线![]() 的斜率;
的斜率;
(ii) 求证: ![]() 的面积与
的面积与![]() 的面积相等.
的面积相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣3x2+a(6﹣a)x+c.
(1)当c=19时,解关于a的不等式f(1)>0;
(2)若关于x的不等式f(x)>0的解集是(﹣1,3),求实数a,c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com