
已知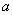 为正实数,
为正实数,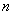 为自然数,抛物线
为自然数,抛物线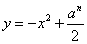 与
与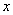 轴正半轴相交于点
轴正半轴相交于点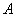 .设
.设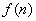 为该抛物线在点
为该抛物线在点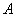 处的切线在
处的切线在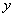 轴上的截距.
轴上的截距.
⑴用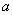 和
和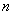 表示
表示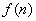 ;
;
⑵求对所有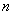 都有
都有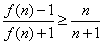 成立的
成立的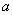 的最小值;
的最小值;
⑶当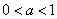 时,比较
时,比较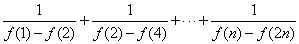 与
与
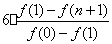 的大小,并说明理由.
的大小,并说明理由.
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
已知点P(x,y)在不等式组 表示的平面区域内运动,则z=x-y的取值范围是( )
表示的平面区域内运动,则z=x-y的取值范围是( )
A.[-2,-1] B.[-2,1] C.[-1,2] D.[1,2]
查看答案和解析>>
科目:高中数学 来源: 题型:
下列说法错误的是 ( )
A.命题:“已知f(x)是R 上的增函数,若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b)”的逆否命题为真命题
上的增函数,若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b)”的逆否命题为真命题
B.“x>1”是“|x|>1”的充分不必要条件 C.若p且q为假命题, 则p、q均为假命题
则p、q均为假命题
 D.命题p:“∃x∈R,使得x2+x+1<0”,则 p:“∀x∈R,均有x2+x+
D.命题p:“∃x∈R,使得x2+x+1<0”,则 p:“∀x∈R,均有x2+x+ 1≥0”
1≥0”

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com