
已知函数f(x)=mx2-mx-1.
(1)若对于x∈R,f(x)<0恒成立,求实数m的取值范围;
(2)若对于x∈[1,3],f(x)<5-m恒成立,求实数m的取值范围.
(1)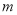 的取值范围
的取值范围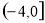 (2)
(2)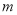 的取值范围
的取值范围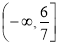
【解析】
试题分析:(1)对于含二次项恒成立的问题,注意讨论二次项系数是否为0,这是学生容易漏掉的地方.(2)恒成立问题一般需转化为最值,利用单调性证明在闭区间的单调性.(3)一元二次不等式在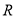 上恒成立,看开口方向和判别式.(4)含参数的一元二次不等式在某区间内恒成立的问题通常有两种处理方法:一是利用二次函数在区间上的最值来处理;二是分离参数,再去求函数的最值来处理,一般后者比较简单.
上恒成立,看开口方向和判别式.(4)含参数的一元二次不等式在某区间内恒成立的问题通常有两种处理方法:一是利用二次函数在区间上的最值来处理;二是分离参数,再去求函数的最值来处理,一般后者比较简单.
试题解析:解析(1)由题意可得m=0或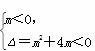 ?m=0或-4<m<0
?m=0或-4<m<0
?-4<m≤0.
故m的取值范围为(-4,0]. 6分
(2)∵f(x)<-m+5?m(x2-x+1)<6,
∵x2-x+1>0,∴m<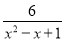 对于x∈[1,3]恒成立,
对于x∈[1,3]恒成立,
记g(x)=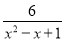 ,x∈[1,3],
,x∈[1,3],
记h(x)=x2-x+1,h(x)在x∈[1,3]上为增函数.则g(x)在[1,3]上为减函数,
∴[g(x)]min=g(3)=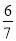 , ∴m<
, ∴m<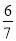 . 所以m的取值范围为
. 所以m的取值范围为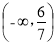 . 3分
. 3分
考点:一元二次不等式恒成立的问题.


 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源:2016届安徽省高一第二学期第一次月考数学试卷(解析版) 题型:选择题
阅读如图所示的程序框图,运行相应的程序.若输入某个正整数n后,输出的S∈(31,72),则n的值为( )
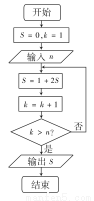
A.5 B.6 C.7 D.8
查看答案和解析>>
科目:高中数学 来源:2016届安徽省高一下学期期末考试数学试卷(解析版) 题型:填空题
已知函数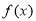 与
与 的定义域为
的定义域为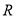 ,有下列5个命题:
,有下列5个命题:
①若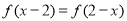 ,则
,则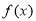 的图象自身关于直线
的图象自身关于直线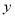 轴对称;
轴对称;
②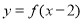 与
与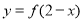 的图象关于直线
的图象关于直线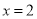 对称;
对称;
 ③函数
③函数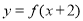 与
与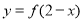 的图象关于
的图象关于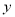 轴对称;
轴对称;
④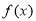 为奇函数,且
为奇函数,且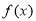 图象关于直线
图象关于直线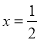 对称,则
对称,则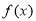 周期为2;
周期为2;
⑤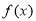 为偶函数,
为偶函数, 为奇函数,且
为奇函数,且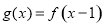 ,则
,则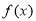 周期为2。
周期为2。
其中正确命题的序号是 。
查看答案和解析>>
科目:高中数学 来源:2016届安徽省高一下学期期中考试数学试卷(解析版) 题型:填空题
在△ABC中,角A,B,C所对的边分别是a,b,c,已知 则C=______________.
则C=______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com