
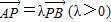 .过A、B两点分别作抛物线的切线,设其交点为M.
.过A、B两点分别作抛物线的切线,设其交点为M.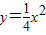 ,求导得
,求导得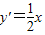
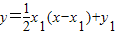
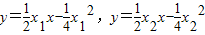 ,联立方程可得
,联立方程可得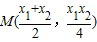 ,由
,由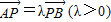 ,得
,得 ,结合抛物线的方程整理可求
,结合抛物线的方程整理可求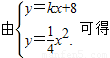 x2-4kx-32=0,x1+x2=4k,x1x2=-32,利用导数知识可得过抛物线上A、B两点的切线斜率分别是
x2-4kx-32=0,x1+x2=4k,x1x2=-32,利用导数知识可得过抛物线上A、B两点的切线斜率分别是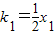 ,
,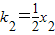 ,从而可写出切线MA.MB的方程,联立方程可求M
,从而可写出切线MA.MB的方程,联立方程可求M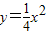 ,求导得
,求导得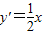
 ,
,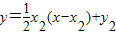 ,即
,即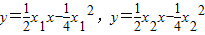 ,解得
,解得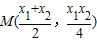 .
.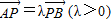 ,得(-x1,8-y1)=λ(x2,y2-8),即
,得(-x1,8-y1)=λ(x2,y2-8),即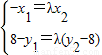 将式(1)两边平方并代入
将式(1)两边平方并代入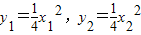 得y1=λ2y2,再代入(2)得λy2=8,解得
得y1=λ2y2,再代入(2)得λy2=8,解得 且有x1x2=-λx22=-4λy2=-32,所以,点M的纵坐标为-8.
且有x1x2=-λx22=-4λy2=-32,所以,点M的纵坐标为-8.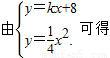 x2-4kx-32=0,x1+x2=4k,x1x2=-32
x2-4kx-32=0,x1+x2=4k,x1x2=-32 .
.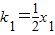 ,
,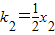 ,∴
,∴
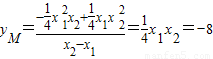
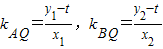 ,
,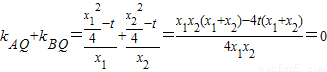 对一切k恒成立
对一切k恒成立

 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
 已知抛物线x2=4y上的点P(非原点)处的切线与x轴,y轴分别交于Q,R两点,F为焦点.
已知抛物线x2=4y上的点P(非原点)处的切线与x轴,y轴分别交于Q,R两点,F为焦点.| PQ |
| PR |
| PF |
| FA |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2009•温州一模)如图,已知抛物线x2=4y,过抛物线上一点A(x1,y1)(不同于顶点)作抛物线的切线l,并交x轴于点C,在直线y=-1上任取一点H,过H作HD垂直x轴于D,并交l于点E,过H作直线HF垂直直线l,并交x轴于点F.
(2009•温州一模)如图,已知抛物线x2=4y,过抛物线上一点A(x1,y1)(不同于顶点)作抛物线的切线l,并交x轴于点C,在直线y=-1上任取一点H,过H作HD垂直x轴于D,并交l于点E,过H作直线HF垂直直线l,并交x轴于点F.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2011•浙江模拟)已知抛物线x2=4y,圆C:x2+(y-2)2=4,M(x0,y0),(x0>0,y0>0)为抛物线上的动点.
(2011•浙江模拟)已知抛物线x2=4y,圆C:x2+(y-2)2=4,M(x0,y0),(x0>0,y0>0)为抛物线上的动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com