
| A. | -1 | B. | 1 | C. | $-\frac{7}{5}$ | D. | $\frac{7}{5}$ |
分析 由复数求模公式和复数的乘法运算化简复数$\frac{{i({-6+i})}}{{|{3-4i}|}}$,求出复数$\frac{{i({-6+i})}}{{|{3-4i}|}}$的实部和虚部,则答案可求.
解答 解:∵$\frac{{i({-6+i})}}{{|{3-4i}|}}$=$\frac{-6i+{i}^{2}}{\sqrt{{3}^{2}+(-4)^{2}}}=\frac{-1-6i}{5}=-\frac{1}{5}-\frac{6}{5}i$,
∴复数$\frac{{i({-6+i})}}{{|{3-4i}|}}$的实部为:$-\frac{1}{5}$,虚部为:$-\frac{6}{5}$,差为:1.
故选:B.
点评 本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1} | B. | {-2,-1} | C. | {-2,-1} | D. | {-3,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
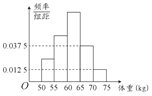 为了了解我校今年报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为12,则报考飞行员的学生人数是( )
为了了解我校今年报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为12,则报考飞行员的学生人数是( )| A. | 50 | B. | 47 | C. | 48 | D. | 52 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 266,14 | B. | 256,14 | C. | 256,-$\frac{21}{4}$ | D. | 266,-4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{4}$,-1) | B. | ($\frac{1}{4}$,1) | C. | ($\frac{1}{2}$,-1) | D. | ($\frac{1}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -1 | C. | 2或-1 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com