
【题目】将2006表示成5个正整数![]() 之和. 记
之和. 记![]() . 问:
. 问:
(1)当![]() 取何值时,S取到最大值;
取何值时,S取到最大值;
(2)进一步地,对任意![]() 有
有![]() ,当
,当![]() 取何值时,S取到最小值. 说明理由.
取何值时,S取到最小值. 说明理由.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据条件,判断S的值是有界集,故必存在最大值与最小值,且S取到最大值,则必有![]() ,从而可求结论;
,从而可求结论;
(2)当![]() ,且
,且![]() 时,只有三种情况,后两种情形是由第一组作
时,只有三种情况,后两种情形是由第一组作![]() 调整下得到的,结合(1)中的分析,可得结论.
调整下得到的,结合(1)中的分析,可得结论.
(1) 首先这样的S的值是有界集,故必存在最大值与最小值。 若![]() , 且使
, 且使 ![]() 取到最大值,则必有
取到最大值,则必有
![]()
![]() (*)
(*)
事实上,假设(*)不成立,不妨假设![]() 。则令
。则令![]() ,
,![]() ,
,![]() (
(![]() ),有
),有![]() ,
,![]() 。
。
将S改写成![]()
![]()
同时有 ![]() 。
。
于是有![]() .这与S在
.这与S在![]() 时取到最大值矛盾.所以必有
时取到最大值矛盾.所以必有![]()
![]() . 因此当
. 因此当![]() 取到最大值.
取到最大值.
(2)当![]() 且
且![]() 时,只有
时,只有
402, 402, 402, 400, 400;
402, 402, 401, 401, 400;
402, 401, 401, 401, 401; 三种情形满足要求。而后面两种情形是在第一组情形下作![]() ,
,![]() 调整下得到的。根据上一小题的证明可以知道,每调整一次,和式
调整下得到的。根据上一小题的证明可以知道,每调整一次,和式![]() 变大. 所以在
变大. 所以在![]() 情形取到最小值.
情形取到最小值.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:

(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数![]() ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的工人数填入下面的列联表:
的工人数填入下面的列联表:
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:![]() ,
,
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,角A、B、C所对的边分别为a、b、c,且2acosB=3b﹣2bcosA. 
(1)求 ![]() 的值;
的值;
(2)设AB的中垂线交BC于D,若cos∠ADC= ![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S—ABCD的底面是正方形,侧棱SA⊥底面ABCD,
过A作AE垂直SB交SB于E点,作AH垂直SD交SD于H点,平面AEH交SC于K点,且AB=1,SA=2.

(1)证明E、H在以AK为直径的圆上,且当点P是SA上任一点时,试求![]() 的最小值;
的最小值;
(2)求平面AEKH与平面ABCD所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义函数F(a,b)= ![]() (a+b﹣|a﹣b|)(a,b∈R),设函数f(x)=﹣x2+2x+4,g(x)=x+2(x∈R)函数F(f(x),g(x))的最大值与零点之和为( )
(a+b﹣|a﹣b|)(a,b∈R),设函数f(x)=﹣x2+2x+4,g(x)=x+2(x∈R)函数F(f(x),g(x))的最大值与零点之和为( )
A.4
B.6
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() . 以坐标原点
. 以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)求直线![]() 的参数方程(设参数为
的参数方程(设参数为![]() )和曲线
)和曲线![]() 的普通方程;
的普通方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,若关于x的方程f2(x)﹣bf(x)+c=0(b,c∈R)有8个不同的实数根,则b+c的取值范围为( )
,若关于x的方程f2(x)﹣bf(x)+c=0(b,c∈R)有8个不同的实数根,则b+c的取值范围为( )
A.(﹣∞,3)
B.(0,3]
C.[0,3]
D.(0,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,⊙O是以AB为直径的圆,点C在圆上,在△ABC和△ACD中,∠ADC=90°,∠BAC=∠CAD,DC的延长线与AB的延长线交于点E.若EB=6,EC=6 ![]() ,则BC的长为 .
,则BC的长为 . 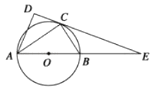
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com