
【题目】设函数![]() (
(![]() 为常数,
为常数, ![]() 为自然对数的底数).
为自然对数的底数).
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 在
在![]() 内存在三个极值点,求实数
内存在三个极值点,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() (2)
(2) .
.
【解析】试题分析:(1)第(1)问,直接求导,再求函数的单调区间. (2)第(2)问,对k进行分类讨论,求出每一种情况下函数的单调性,再分析函数![]() 在
在![]() 内存在三个极值点的条件从而得到实数k的取值范围.
内存在三个极值点的条件从而得到实数k的取值范围.
试题解析:
(1) 函数![]() 的定义域为
的定义域为![]() .
.![]() .
.
由![]() 可得
可得![]() ,所以当
,所以当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
故![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]()
(2)由(1)知,当![]() 时,函数
时,函数![]() 在
在![]() 内单调递减,在
内单调递减,在![]() 内单调递增,故
内单调递增,故![]() 在
在![]() 内仅存在一个极值点
内仅存在一个极值点![]() ;
;
当![]() 时,令
时,令![]() ,
, ![]() ,依题函数
,依题函数![]() 与函数
与函数![]() ,
, ![]() 的图象有两个横坐标不等于2的交点.
的图象有两个横坐标不等于2的交点.

![]() ,当
,当![]() 时,
时, ![]() ,则
,则![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时, ![]() ,则
,则![]() 在
在![]() 上单调递增;
上单调递增;
而![]()
所以当![]() 即
即![]() 时,存在
时,存在![]() 使得
使得![]() ,
,
且当![]() 时
时![]() ,当
,当![]()
![]() ,当
,当![]() 时
时![]() ,当
,当时
![]() ,此时
,此时![]() 存在极小值点
存在极小值点![]() 和极大值点
和极大值点![]() ;
;
同理,当![]() 即
即![]() 时,存在
时,存在![]() 使得
使得![]() ,此时
,此时![]() 存在极小值点
存在极小值点![]() 和极大值点
和极大值点![]() .
.
综上,函数![]() 在
在![]() 内存在三个极值点时,实数
内存在三个极值点时,实数![]() 的取值范围为
的取值范围为 .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+ ![]() ,曲线y=f(x)在点(1,f(1))处的切线方程为y=2.
,曲线y=f(x)在点(1,f(1))处的切线方程为y=2.
(I)求a、b的值;
(Ⅱ)当x>1时,不等式f(x)> ![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是直角梯形,∠ABC=∠BCD= ![]() ,AB=BC=1,CD=2,PA⊥平面ABCD,E是PD的中点.
,AB=BC=1,CD=2,PA⊥平面ABCD,E是PD的中点. 
(1)求证:AE∥平面PBC;
(2)若直线AE与直线BC所成角等于 ![]() ,求二面角D﹣PB﹣A平面角的余弦值.
,求二面角D﹣PB﹣A平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)经过点P(﹣2,0)与点(1,1).
=1(a>b>0)经过点P(﹣2,0)与点(1,1).
(1)求椭圆的方程;
(2)过P点作两条互相垂直的直线PA,PB,交椭圆于A,B.
①证明直线AB经过定点;
②求△ABP面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为建立健全国家学生体质健康监测评价机制,激励学生积极参加身体锻炼,教育部印发《国家学生体质健康标准(2014年修订)》,要求各学校每学期开展覆盖本校各年级学生的《标准》测试工作,并根据学生每个学期总分评定等级.某校决定针对高中学生,每学期进行一次体质健康测试,以下是小明同学六个学期体质健康测试的总分情况.
学期 | 1 | 2 | 3 | 4 | 5 | 6 |
总分 | 512 | 518 | 523 | 528 | 534 | 535 |
(1)请根据上表提供的数据,用相关系数![]() 说明
说明![]() 与
与![]() 的线性相关程度,并用最小二乘法求出
的线性相关程度,并用最小二乘法求出![]() 关于
关于![]() 的线性回归方程(线性相关系数保留两位小数);
的线性回归方程(线性相关系数保留两位小数);
(2)在第六个学期测试中学校根据 《标准》,划定540分以上为优秀等级,已知小明所在的学习小组10个同学有6个被评定为优秀,测试后同学们都知道了自己的总分但不知道别人的总分,小明随机的给小组内4个同学打电话询问对方成绩,优秀的同学有![]() 人,求
人,求![]() 的分布列和期望.
的分布列和期望.
参考公式: 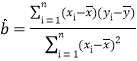 ,
,![]() ;
;
相关系数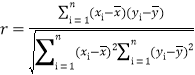 ;
;
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将2006表示成5个正整数![]() 之和. 记
之和. 记![]() . 问:
. 问:
(1)当![]() 取何值时,S取到最大值;
取何值时,S取到最大值;
(2)进一步地,对任意![]() 有
有![]() ,当
,当![]() 取何值时,S取到最小值. 说明理由.
取何值时,S取到最小值. 说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年8月31日下午,关于修改个人所得税法的决定经十三届全国人大常委会第五次会议表决通过。2018年10月1日起施行最新起征点和税率。个税起征点提高至每月5000元.设个人月应纳税所得额为![]() 元,个人月工资收入为
元,个人月工资收入为![]() 元,三险金(养老保险、失业保险、医疗保险、住房公积金)及其它各类免税额总计为
元,三险金(养老保险、失业保险、医疗保险、住房公积金)及其它各类免税额总计为![]() 元,则
元,则![]() .设月应纳税额为
.设月应纳税额为![]() ,个税的计算方式一般是分级计算求总和 (如图表所示,共分7级).比如:小陈的应纳税所得额为
,个税的计算方式一般是分级计算求总和 (如图表所示,共分7级).比如:小陈的应纳税所得额为![]() 元,月应交纳税额为
元,月应交纳税额为![]() 元.
元.
税级 | 月应纳税所得额 | 税率 |
1 |
| 3% |
2 |
| 10% |
3 |
| 20% |
4 |
| 25% |
5 |
| 30% |
6 |
| 35% |
7 |
| 45% |
(1)小王的应纳税所得额![]() 元,求
元,求![]() ;
;
(2)小张的应纳税所得额![]() 元,若
元,若![]() 元,求
元,求![]() ;
;
(3)当![]() 时,写出
时,写出![]() 的解析式(请写成分段函数的形式).
的解析式(请写成分段函数的形式).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com