
【题目】十九大提出对农村要坚持精准扶贫,至2020年底全面脱贫.现有扶贫工作组到某山区贫困村实施脱贫工作.经摸底排查,该村现有贫闲农户100家,他们均从事水果种植,2017年底该村平均每户年纯收入为1万元.扶贫工作组一方面请有关专家对果树进行品种改良,提高产量;另一方面,抽出部分农户从事水果包装、销售工作,其人数必须小于种植的人数.从2018年初开始,该村抽出![]() 户(
户(![]() )从事水果包装、销售.经测算,剩下从事水果种植农户的年纯收入每户平均比上一年提高
)从事水果包装、销售.经测算,剩下从事水果种植农户的年纯收入每户平均比上一年提高![]() ,而从事包装销售农户的年纯收入每户平均为
,而从事包装销售农户的年纯收入每户平均为![]() 万元(参考数据:
万元(参考数据:![]() ).
).
(1)至2020年底,为使从事水果种植农户能实现脱贫(每户年均纯收入不低于1万5千元),则应至少抽出多少户从事包装、销售工作?
(2)至2018年底,该村每户年均纯收人能否达到1.355万元?若能,请求出从事包装、销售的户数;若不能,请说明理由.
【答案】(1)15(2)当从事包装、销售的户数达到20户、25户、30户时,能达到,否则不能,理由见解析
【解析】
(1)根据从事水果种植农户的年纯收入每户平均比上一年提高![]() 列式求解即可得出
列式求解即可得出![]() 的值,继而得出从事包装、销售工作的户数.
的值,继而得出从事包装、销售工作的户数.
(2)根据题意计算从事水果种植农户的年纯收入与从事包装、销售工作的农户的总和除以总人数100即可得该村每户年均纯收入,再列出不等式求解即可.
(1)至2020年底,种植户平均收入![]() ,
,
即![]() ,由题所给数据,
,由题所给数据,
知:![]() ,所以,
,所以,![]() ,
,
所以,x的最小值为3,![]() ,
,
即至少抽出15户从事包装、销售工作.
(2)至2018年底,假设能达到1.355万元,
每户的平均收入为: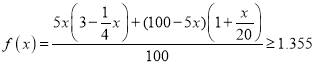 ,
,
化简,得:![]() ,因为
,因为![]()
解得:![]() .
.
所以,当从事包装、销售的户数达到20户、25户、30户时,能达到,
否则不能.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 左顶点为M,上顶点为N,直线MN的斜率为
左顶点为M,上顶点为N,直线MN的斜率为![]() .
.
(Ⅰ)求椭圆的离心率;
(Ⅱ)直线l:![]() 与椭圆交于A,C两点,与y轴交于点P,以线段AC为对角线作正方形ABCD,若
与椭圆交于A,C两点,与y轴交于点P,以线段AC为对角线作正方形ABCD,若![]() .
.
(![]() )求椭圆方程;
)求椭圆方程;
(![]() )若点E在直线MN上,且满足
)若点E在直线MN上,且满足![]() ,求使得
,求使得![]() 最长时,直线AC的方程.
最长时,直线AC的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() ,且
,且![]() 为等边三角形,若四棱锥
为等边三角形,若四棱锥![]() 的体积与四棱锥
的体积与四棱锥![]() 外接球的表面积大小之比为
外接球的表面积大小之比为![]() ,则四棱锥
,则四棱锥![]() 的表面积为___________.
的表面积为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列五个命题:
①已知直线![]() 、
、![]() 和平面
和平面![]() ,若
,若![]() ,
,![]() ,则
,则![]() ;
;
②平面上到一个定点和一条定直线的距离相等的点的轨迹是一条抛物线;
③双曲线![]() ,则直线
,则直线![]()
![]() 与双曲线有且只有一个公共点;
与双曲线有且只有一个公共点;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直;
⑤过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 中点为
中点为![]() ,设直线
,设直线![]() 斜率为
斜率为![]()
![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,则
,则![]() 等于
等于![]() .
.
其中,正确命题的序号为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为 为参数
为参数![]() ,以坐标原点O为极点,以x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为
,以坐标原点O为极点,以x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为![]() .
.
![]() 求直线l的普通方程及曲线C的直角坐标方程;
求直线l的普通方程及曲线C的直角坐标方程;
![]() 若直线l与曲线C交于A,B两点,求线段AB的中点P到坐标原点O的距离.
若直线l与曲线C交于A,B两点,求线段AB的中点P到坐标原点O的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人某天的工作是:驾车从![]() 地出发,到
地出发,到![]() 两地办事,最后返回
两地办事,最后返回![]() 地,
地,![]() 三地之间各路段行驶时间及当天降水概率如表:
三地之间各路段行驶时间及当天降水概率如表:
路段 | 正常行驶所需时间(小时) | 上午降水概率 | 下午降水概率 |
| 2 | 0.3 | 0.6 |
| 2 | 0.2 | 0.7 |
| 3 | 0.3 | 0.9 |
若在某路段遇到降水,则在该路段行驶的时间需延长1小时,现有如下两个方案:
方案甲:上午从![]() 地出发到
地出发到![]() 地办事,然后到达
地办事,然后到达![]() 地,下午在
地,下午在![]() 地办事后返回
地办事后返回![]() 地;
地;
方案乙:上午从![]() 地出发到
地出发到![]() 地办事,下午从
地办事,下午从![]() 地出发到达
地出发到达![]() 地, 办事后返回
地, 办事后返回![]() 地.
地.
(1)设此人8点从![]() 地出发,在各地办事及午餐的累积时间为2小时.且采用方案甲,求他当日18点或18点之前能返回
地出发,在各地办事及午餐的累积时间为2小时.且采用方案甲,求他当日18点或18点之前能返回![]() 地的概率;
地的概率;
(2)甲、乙两个方案中,哪个方案有利于办完事后能更早返回![]() 地?
地?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com