
【题目】已知函数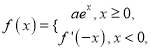 曲线
曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() ;
;
(2)若存在实数![]() ,对任意的
,对任意的![]() ,都有
,都有![]() ,求整数
,求整数![]() 的最小值.
的最小值.
科目:高中数学 来源: 题型:
【题目】如图,已知梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 为矩形,
为矩形, ![]() ,平面
,平面![]() 平面
平面![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出线段
,若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD= ![]() .
.
(Ⅰ)求证:PD⊥平面PAB;
(Ⅱ)求直线PB与平面PCD所成角的正弦值;
(Ⅲ)在棱PA上是否存在点M,使得BM∥平面PCD?若存在,求 ![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.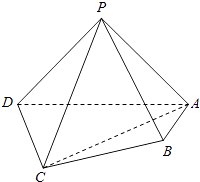
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|,g(x)=x2+2ax+1(a为正常数),且函数f(x)和g(x)的图象与y轴的交点重合.
(1)求a实数的值
(2)若h(x)=f(x)+b ![]() (b为常数)试讨论函数h(x)的奇偶性;
(b为常数)试讨论函数h(x)的奇偶性;
(3)若关于x的不等式f(x)﹣2 ![]() >a有解,求实数a的取值范围.
>a有解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(Ⅰ)当每辆车的月租金定为3600元时,能租出多少辆车?
(Ⅱ)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点O,焦点在![]() 轴上,离心率为
轴上,离心率为![]() 的椭圆C过点
的椭圆C过点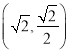
(Ⅰ)求椭圆C的方程;
(Ⅱ)设不过坐标原点O的直线与椭圆C交于P,Q两点,若![]() ,证明:点O到直线
,证明:点O到直线![]() 的距离为定值.
的距离为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆曲线方程为 ![]() ,两焦点分别为F1 , F2 .
,两焦点分别为F1 , F2 .
(1)若n=﹣1,过左焦点为F1且斜率为 ![]() 的直线交圆锥曲线于点A,B,求△ABF2的周长.
的直线交圆锥曲线于点A,B,求△ABF2的周长.
(2)若n=4,P圆锥曲线上一点,求PF1PF2的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x2+ax+b,且f(4)=﹣3.
(1)若函数f(x)在区间[2,+∞)上递减,求实数b的取值范围;
(2)若函数f(x)的图象关于直线x=1对称,且关于x的方程f(x)=log2m在区间[﹣3,3]上有解,求m的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com