
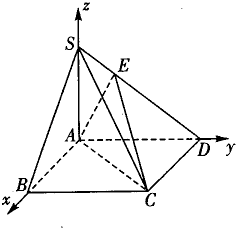
【题目】在直角梯形PBCD中, ![]() ,A为PD的中点,如图.将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,且
,A为PD的中点,如图.将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,且 ![]() ,如图.
,如图.
(Ⅰ)求证:SA⊥平面ABCD;
(Ⅱ)求二面角E﹣AC﹣D的正切值.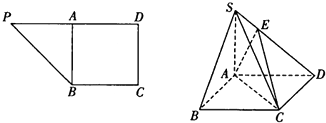
【答案】解法一:(Ⅰ)证明:在题平面图形中,由题意可知,BA⊥PD,ABCD为正方形,所以在翻折后的图中,SA⊥AB,SA=2,四边形ABCD是边长为2的正方形,
因为SB⊥BC,AB⊥BC,SB∩AB=B
所以BC⊥平面SAB,
又SA平面SAB,
所以BC⊥SA,
又SA⊥AB,BC∩AB=B
所以SA⊥平面ABCD,
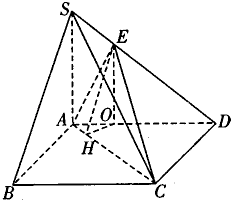
(Ⅱ)在AD上取一点O,使 ![]() ,连接EO
,连接EO
因为 ![]() ,所以EO∥SA
,所以EO∥SA
因为SA⊥平面ABCD,
所以EO⊥平面ABCD,
过O作OH⊥AC交AC于H,连接EH,
则AC⊥平面EOH,
所以AC⊥EH.
所以∠EHO为二面角E﹣AC﹣D的平面角, ![]() .
.
在Rt△AHO中, ![]()
∴ ![]() ,
,
即二面角E﹣AC﹣D的正切值为 ![]()
解法二:(Ⅰ)同方法一
(Ⅱ)解:如图,以A为原点建立直角坐标系,A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),S(0,0,2),E(0, ![]() )
)
∴平面ACD的法向为 ![]()
设平面EAC的法向量为 ![]() =(x,y,z),
=(x,y,z), ![]()
由 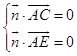 ,
,
所以 ![]() ,可取
,可取 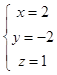
所以 ![]() =(2,﹣2,1).
=(2,﹣2,1).
所以 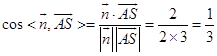
所以 ![]()
即二面角E﹣AC﹣D的正切值为 ![]()
【解析】(法一)(Ⅰ)由题意可知,翻折后的图中SA⊥AB①,易证BC⊥SA②,由①②根据直线与平面垂直的判定定理可得SA⊥平面ABCD;(Ⅱ)(三垂线法)由 ![]() 考虑在AD上取一点O,使得
考虑在AD上取一点O,使得 ![]() ,从而可得EO∥SA,所以EO⊥平面ABCD,过O作OH⊥AC交AC于H,连接EH,∠EHO为二面角E﹣AC﹣D的平面角,在Rt△AHO中求解即可(法二:空间向量法)(Ⅰ)同法一(Ⅱ)以A为原点建立直角坐标系,易知平面ACD的法向为
,从而可得EO∥SA,所以EO⊥平面ABCD,过O作OH⊥AC交AC于H,连接EH,∠EHO为二面角E﹣AC﹣D的平面角,在Rt△AHO中求解即可(法二:空间向量法)(Ⅰ)同法一(Ⅱ)以A为原点建立直角坐标系,易知平面ACD的法向为 ![]() ,求平面EAC的法向量,代入公式求解即可
,求平面EAC的法向量,代入公式求解即可


科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ![]() ,过左焦点F1(﹣c,0)作圆x2+y2=a2的切线,切点为E,延长F1E交抛物线y2=4cx于P,Q两点,则|PE|+|QE|的值为( )
,过左焦点F1(﹣c,0)作圆x2+y2=a2的切线,切点为E,延长F1E交抛物线y2=4cx于P,Q两点,则|PE|+|QE|的值为( )
A.![]()
B.10a
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sin2x的图象向左![]() 平移个单位,向上平移1个单位,得到的函数解析式为( )
平移个单位,向上平移1个单位,得到的函数解析式为( )
A.y=sin(2x+![]() )+1
)+1
B.y=sin(2x﹣![]() )+1
)+1
C.y=sin(2x+![]() )+1
)+1
D.y=sin(2x﹣![]() )+1
)+1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(理)如图,在正方体ABCD﹣A1B1C1D1中,点O为线段BD的中点.设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( ) 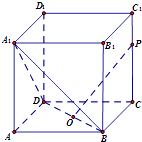
A.[ ![]() ,1]
,1]
B.[ ![]() ,1]
,1]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,1]
,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,点M在AB上,且AM:MB=1:2,E为PB的中点. 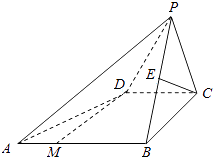
(1)求证:CE∥平面ADP;
(2)求证:平面PAD⊥平面PAB;
(3)棱AP上是否存在一点N,使得平面DMN⊥平面ABCD,若存在,求出 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,PA⊥⊙O所在平面,AB是⊙O的直径,C是⊙O上一点,AE⊥PC,AF⊥PB,给出下列结论:①AE⊥BC;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC,其中真命题的序号是 . 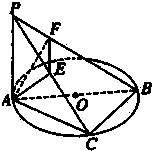
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合{φ|f(x)=sin[(x﹣2φ)π]+cos[(x﹣2φ)π]为奇函数,且|logaφ|<1}的子集个数为4,则a的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=ax2﹣2ax+1+b(a≠0,b<1),在区间[2,3]上有最大值4,最小值1,设f(x)= ![]() .
.
(1)求a,b的值;
(2)不等式f(2x)﹣k2x≥0在x∈[﹣1,1]上恒成立,求实数k的取值范围;
(3)方程f(|2x﹣1|)+k( ![]() ﹣3)有三个不同的实数解,求实数k的取值范围.
﹣3)有三个不同的实数解,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com