
【题目】如图,正三棱柱 ![]() 中,
中, ![]() 是
是 ![]() 的中点.
的中点.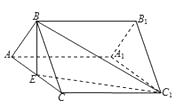
(1)求证:平面 ![]() ;
;
(2)若 ![]() ,求点
,求点 ![]() 到平面
到平面 ![]() 的距离.
的距离.
【答案】
(1)证明:∵ ![]() 是正三棱柱,
是正三棱柱,
∴ ![]() 平面
平面 ![]() ,又
,又 ![]() 平面
平面 ![]() ,∴
,∴ ![]() .∵
.∵ ![]() 是正三角形,
是正三角形, ![]() 是
是 ![]() 中点,
中点,
∴ ![]() ,又
,又 ![]() ,
, ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,
,
∴ ![]() 平面
平面 ![]() ,
,
∵ ![]() 平面
平面 ![]() ,
,
∴平面 ![]() ⊥平面
⊥平面 ![]()
(2)解 : 正三棱柱 ![]() 中,
中, ![]() ,因为
,因为 ![]() 是
是 ![]() 中点,
中点,
∴ ![]() ,
,
∴ ![]() .
.
在直角 ![]() 中,
中, ![]() ,
,
∵ ![]() 平面
平面 ![]() ,
,
![]() 平面
平面 ![]() ,∴
,∴ ![]() ,
,
∴ ![]() .
.
设点 ![]() 到面
到面 ![]() 的距离为
的距离为 ![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,
,
∴ ![]() .
.
【解析】(1)由题意结合正三棱柱的性质可知A A1 ⊥ 平面 A B C进而得到 B E ⊥ A A1,由 Δ A B C 是正三角形 E 是 A C 中点,可得B E ⊥ A C 再由线面垂直的判定定理可得出B E ⊥ 平面 A C C1 A1,进而得到面面垂直。(2)根据题意可知点A到平面BEC1的距离即点C到平面BEC1的距离,过点C作出![]() ,则可证CH垂直于平面BEC1,故CH为点 C到平面 B E C1的距离即为点 A 到平面 B E C1的距离.
,则可证CH垂直于平面BEC1,故CH为点 C到平面 B E C1的距离即为点 A 到平面 B E C1的距离.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AC=2 ![]() ,AA1=
,AA1= ![]() ,AB=2,点D在棱B1C1上,且B1C1=4B1D (Ⅰ)求证:BD⊥A1C
,AB=2,点D在棱B1C1上,且B1C1=4B1D (Ⅰ)求证:BD⊥A1C
(Ⅱ)求二面角B﹣A1D﹣C的大小.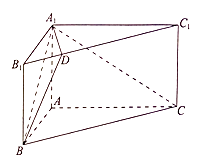
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一房产商竞标得一块扇形OPQ地皮,其圆心角∠POQ= ![]() ,半径为R=200m,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形ABCD的一边AB在半径OP上,C在圆弧上,D在半径OQ;方案二:矩形EFGH的顶点在圆弧上,顶点G,H分别在两条半径上.请你通过计算,为房产商提供决策建议.
,半径为R=200m,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形ABCD的一边AB在半径OP上,C在圆弧上,D在半径OQ;方案二:矩形EFGH的顶点在圆弧上,顶点G,H分别在两条半径上.请你通过计算,为房产商提供决策建议. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有( )
A.a>b>c
B.b>c>a
C.c>a>b
D.c>b>a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三条不重合的直线 ![]() 和两个不重合的平面
和两个不重合的平面 ![]() ,下列命题正确的是( )
,下列命题正确的是( )
A.若 ![]() ,
, ![]() ,则
,则 ![]()
B.若 ![]() ,
, ![]() ,且
,且 ![]() ,则
,则 ![]()
C.若 ![]() ,
, ![]() ,则
,则 ![]()
D.若 ![]() ,
, ![]() ,且
,且 ![]() ,则
,则 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形PBCD中, ![]() ,A为PD的中点,如图.将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,且
,A为PD的中点,如图.将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,且 ![]() ,如图.
,如图.
(Ⅰ)求证:SA⊥平面ABCD;
(Ⅱ)求二面角E﹣AC﹣D的正切值.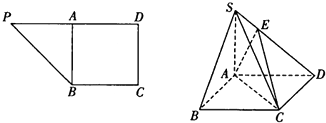
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是( ) 
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() ]
]
C.( ![]() ,
, ![]() ]
]
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com