
分析 根据通项公式可得当$\frac{60-r}{2}$ 和$\frac{r}{4}$都是整数时,才会得到有理项,故r=0,4,8,12,…,60时,得到有理项,从而得出结论.
解答 解:在($\sqrt{2}$+$\root{4}{3}$)60展开式的通项公式为Tr+1=${C}_{60}^{r}$•${2}^{\frac{60-r}{2}}$•${3}^{\frac{r}{4}}$,
故当$\frac{60-r}{2}$ 和$\frac{r}{4}$都是整数时,才会得到有理项,
∴r=0,4,8,12,…,60时,得到有理项,共计16项,
故答案为:16.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,属于基础题


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 都不是红球 | B. | 恰有1个红球 | C. | 至少有1个红球 | D. | 至多有1个红球 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,7) | B. | (-9,2) | C. | ( 3,7) | D. | (2,9) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
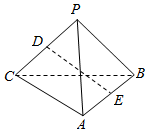 如图,P是平面ABC外一点,PA=4,BC=2$\sqrt{5}$,D,E分别为PC和AB的中点,且DE=3.求异面直线PA和BC所成角的大小.
如图,P是平面ABC外一点,PA=4,BC=2$\sqrt{5}$,D,E分别为PC和AB的中点,且DE=3.求异面直线PA和BC所成角的大小.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com