
(本小题满分12分)如图,在四棱锥P-ABCD中,PD?平面ABCD,AD=CD, DB平分∠ADC,E为PC的中点.
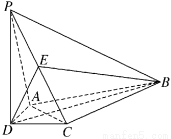
(Ⅰ)证明:PA∥平面BDE;
(Ⅱ)证明:AC?平面PBD.
(Ⅰ)(Ⅱ)见解析.
【解析】
试题分析:(Ⅰ)利用判定定理证明线面平行时,关键是在平面内找一条与已知直线平行的直线,解题时可先直观判断平面内是否已有,若没有,则需作出该直线,常考虑三角形的中位线、平行四边形的对边或过平行线分线段成比例等.(Ⅱ)证明直线和平面垂直的常用方法(1)利用判定定理.(2)利用判定定理的推论(a∥b,a⊥α b⊥α).(3)利用面面平行的性质(a⊥α,α∥β
b⊥α).(3)利用面面平行的性质(a⊥α,α∥β a⊥β).(4)利用面面垂直的性质.
a⊥β).(4)利用面面垂直的性质.
试题解析:(Ⅰ )证明:设AC∩BD=H,连结EH.
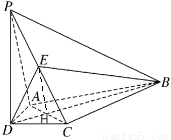
在△ADC中,∵AD=CD,且DB平分∠ADC,
∴H为AC的中点.
又由题设,E为PC的中点,故EH∥PA.
又EH?平面BDE,且PA?平面BDE,
∴PA∥平面BDE. 6分
(Ⅱ)证明:∵PD?平面ABCD,AC?平面ABCD,∴PD?AC.
由(1)可得,DB?AC.
又PD∩DB=D,故AC?平面PBD. 12分
考点:线面平行、垂直的判定.


科目:高中数学 来源:2014-2015学年广东省高一上学期阶段一考试数学试卷(解析版) 题型:选择题
设集合A={x|0≤x≤6},B={y|0≤y≤2},从A到B的对应法则f不是映射的是( ).
A. f:x→y= x B. f:x→y=
x B. f:x→y= x C. f:x→y=
x C. f:x→y=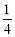 x D. f:x→y=
x D. f:x→y= x
x
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省高一上学期期初考试数学试卷(解析版) 题型:选择题
函数y=ax-2(a>0,a≠1)的图象必经过点( )
A.(0,1) B.(1,1) C.(2,0) D.(2,1)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山西省等校高二上学期期中联考文科数学试卷(解析版) 题型:填空题
一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别是1,2,
3,则此球的表面积为____________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山西省等校高二上学期期中联考文科数学试卷(解析版) 题型:选择题
已知直线a2x+y+2=0与直线bx-(a2+1)y-1=0互相垂直,则|ab|的最小值为
A.5 B.4 C.2 D.1
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山西省高二上学期期中考试文科数学试卷(解析版) 题型:选择题
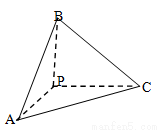
三棱锥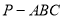 中,三侧棱
中,三侧棱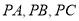 两两互相垂直,且三角形
两两互相垂直,且三角形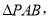
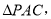
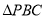 的面积依次为1,1,2,则此三棱锥
的面积依次为1,1,2,则此三棱锥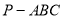 外接球的表面积为
外接球的表面积为
A.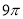 B.
B.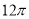 C.
C.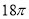 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com