
【题目】某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .估计该校学生每周平均体育运动时间超过6个小时的概率.
.估计该校学生每周平均体育运动时间超过6个小时的概率.
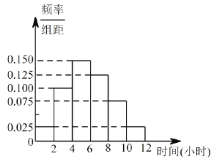
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
|
|
|
|
|
|
|
|
|
|
附: .
.
【答案】(1)90位(2)![]() (3)填表见解析;有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”
(3)填表见解析;有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”
【解析】
(1)根据频率分布直方图进行求解即可;
(2)由频率分布直方图先求出对应的频率,即可估计对应的概率;
(3)利用独立性检验进行求解即可.
(1)![]() .所以,应该收集90位女生的样本数据.
.所以,应该收集90位女生的样本数据.
(2)由频率分布直方图得![]()
所以该校学生每周平均体育运动时间超过6小时的概率的估计值为![]() .
.
(3)每周平均运动时间超过4小时的频率为0.375×2=0.75,所以超过4小时的总人数为300×0.75=225,
每周平均运动时间与性别列联表如下:
男生超过4小时 | 运动不超过4小时 | 合计 | |
男生 | 165 | 45 | 210 |
女生 | 60 | 30 | 90 |
合计 | 225 | 75 | 300 |
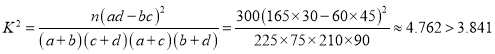 ,
,
所以,有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.


 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,侧面![]() 底面ABCD,
底面ABCD,![]() ,
,![]() ,E,Q分别是BC和PC的中点.
,E,Q分别是BC和PC的中点.
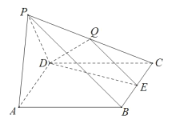
(I)求直线BQ与平面PAB所成角的正弦值;
(Ⅱ)求二面角E-DQ-P的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙两人进行定点投篮活动,已知他们每投篮一次投中的概率分别是![]() 和
和![]() ,每次投篮相互独立互不影响.
,每次投篮相互独立互不影响.
(Ⅰ)甲乙各投篮一次,记“至少有一人投中”为事件A,求事件A发生的概率;
(Ⅱ)甲乙各投篮一次,记两人投中次数的和为X,求随机变量X的分布列及数学期望;
(Ⅲ)甲投篮5次,投中次数为ξ,求ξ=2的概率和随机变量ξ的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2011年,国际数学协会正式宣布,将每年的3月14日设为“国际数学节”,其来源是中国古代数学家祖冲之的圆周率,为庆祝该节日,某校举办的“数学嘉年华”活动中,设计了如下的有奖闯关游戏:参赛选手按第一关、第二关、第三关的顺序依次闯关,若闯关成功,则分别获得5个、10个、20个学豆的奖励.游戏还规定:当选手闯过一关后,可以选择带走相应的学豆,结束游戏;也可以选择继续闯下一关,若有任何一关没有闯关成功,则全部学豆归零,游戏结束.设选手甲能闯过第一关、第二关、第三关的概率分别为![]() ,选手选择继续闯关的概率均为
,选手选择继续闯关的概率均为![]() ,且各关之间闯关成功与否互不影响.
,且各关之间闯关成功与否互不影响.
(1)求选手甲第一关闯关成功且所得学豆为零的概率;
(2)设该选手所得学豆总数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 市某机构为了调查该市市民对我国申办
市某机构为了调查该市市民对我国申办![]() 年足球世界杯的态度,随机选取了
年足球世界杯的态度,随机选取了![]() 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
支持 | 不支持 | 合计 | |
男性市民 |
| ||
女性市民 |
| ||
合计 |
|
|
(1)根据已知数据,把表格数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
(i)能否在犯错误的概率不超过![]() 的前提下认为支持申办足球世界杯与性别有关;
的前提下认为支持申办足球世界杯与性别有关;
(ii)已知在被调查的支持申办足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教师,现从这
位是教师,现从这![]() 位退休老人中随机抽取
位退休老人中随机抽取![]() 人,求至多有
人,求至多有![]() 位老师的概率.
位老师的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆锥![]() (其中
(其中![]() 为顶点,
为顶点,![]() 为底面圆心)的侧面积与底面积的比是
为底面圆心)的侧面积与底面积的比是![]() ,则圆锥
,则圆锥![]() 与它外接球(即顶点在球面上且底面圆周也在球面上)的体积比为( )
与它外接球(即顶点在球面上且底面圆周也在球面上)的体积比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在 △ABC 中,设 a,b,c 分别是角 A,B,C 的对边,已知向量 ![]() = (a,sinC-sinB),
= (a,sinC-sinB),![]() = (b + c,sinA + sinB),且
= (b + c,sinA + sinB),且![]()
(1) 求角 C 的大小
(2) 若 c = 3, 求 △ABC 的周长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网购平台为了解某市居民在该平台的消费情况,从该市使用其平台且每周平均消费额超过100元的人员中随机抽取了100名,并绘制如图所示频率分布直方图,已知中间三组的人数可构成等差数列.
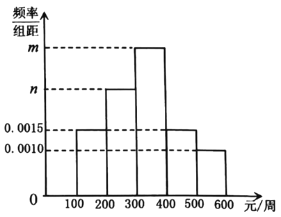
(1)求![]() 的值;
的值;
(2)分析人员对100名调查对象的性别进行统计发现,消费金额不低于300元的男性有20人,低于300元的男性有25人,根据统计数据完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为消费金额与性别有关?
的把握认为消费金额与性别有关?
(3)分析人员对抽取对象每周的消费金额![]() 与年龄
与年龄![]() 进一步分析,发现他们线性相关,得到回归方程
进一步分析,发现他们线性相关,得到回归方程![]() .已知100名使用者的平均年龄为38岁,试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
.已知100名使用者的平均年龄为38岁,试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
![]() 列联表
列联表
男性 | 女性 | 合计 | |
消费金额 | |||
消费金额 | |||
合计 |
临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]() ,其中
,其中![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com