练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若为奇数，则被9除得的余数是…（    ）

    A. 0            B. 2             C. 7              D. 8


    C


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


        已知函数．

    （1）当时，求函数的单调区间；

    （2）若函数在处取得极值，对,恒成立，求实数的取值范围；

    （3）当时，求证：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    从4名男生和3名女生中选出4人参加某个座谈会，若这4人中必须既有男生又有女生，则不同的选法共有(      )

    A、140种      B、120种       C、35种       D、34种

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在三棱锥S—ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，SA=SC=2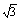，M、N分别为AB、SB的中点， 求点B到平面CMN的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     设口袋中有黑球、白球共7个，从中任取2个球，已知取到白球个数的数学期望值为，则口袋中白球的个数为 …………………………………… …(　 　)

    A．3           B．4              C．5               D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某单位拟安排6位员工在今年5月1日至3日（劳动节假期）值班，每天安排2人，每人值班1天 . 若6位员工中的甲不值1日，乙不值2日，则不同的安排方法共有         种（用数字作答）

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如果执行右边的程序框图，输入，那么输出的各个数的和等于………………………………………………………………………………(    )

    A．        B．         C．        D．

     


    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某大学开设甲、乙、丙三门选修课，学生是否选修哪门课程互不影响，已知某学生只选修甲的概率为0.08，只选修甲和乙的概率是0.12，至少选修一门的概率是0.88，用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积．

    (1)记“函数f(x)＝x2＋ξx为R上的偶函数”为事件A，求事件A的概率；

    (2)求ξ的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列中，，对于，以为系数的一元二次方程

      都有实数根，且满足.

    （Ⅰ）求证：数列是等比数列；

    （Ⅱ）求数列的通项公式；        （Ⅲ）求的前项和.

    查看答案和解析>>

    同步练习册答案