
已知 为实数,则
为实数,则 是关于
是关于 的绝对值不等式
的绝对值不等式 有解的( )
有解的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
B
【解析】
试题分析:由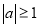 得:
得: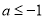 或
或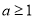 ,因为关于
,因为关于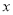 的绝对值不等式
的绝对值不等式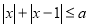 有解集,而
有解集,而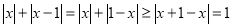 ,所以
,所以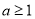 ,所以
,所以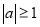 是关于
是关于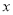 的绝对值不等式
的绝对值不等式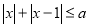 有解的必要不充分条件,故选B.
有解的必要不充分条件,故选B.
考点:1、绝对值不等式;2、充分与必要条件.
考点分析: 考点1:必要条件、充分条件与充要条件的判断 【知识点的认识】正确理解和判断充分条件、必要条件、充要条件和非充分非必要以及原命题、逆命题否命题、逆否命题的概念是本节的重点;掌握逻辑推理能力和语言互译能力,对充要条件概念本质的把握是本节的难点.

科目:高中数学 来源:2014-2015学年贵州省贵阳市高三上学期期末监测考试理科数学试卷(解析版) 题型:选择题
为得到函数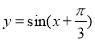 的图象,可将函数
的图象,可将函数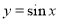 的图象向左平移
的图象向左平移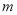 个单位长度,或向右平移
个单位长度,或向右平移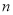 个单位长度(
个单位长度(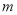 ,
,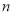 均为正整数),则
均为正整数),则 的最小值是( )
的最小值是( )
A.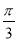 B.
B.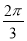 C.
C.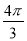 D.
D.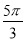
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省龙岩市非一级达标校高三上学期期末检查理科数学试卷(解析版) 题型:填空题
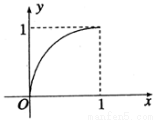
已知定义在区间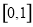 上的函数
上的函数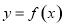 的图象如图所示,对于满足
的图象如图所示,对于满足 的任意
的任意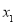 ,
,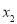 ,给出下列结论:
,给出下列结论:
①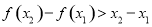 ;
;
②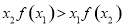 ;
;
③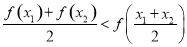 ;
;
④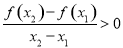 .
.
其中正确结论的序号是 .(把所有正确结论的序号都填上)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省广州市毕业班综合测试一理科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知数列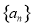 的各项均为正数,其前
的各项均为正数,其前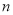 项和为
项和为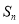 ,且满足
,且满足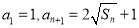 ,
,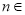 N
N .
.
(1)求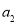 的值;
的值;
(2)求数列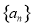 的通项公式;
的通项公式;
(3)是否存在正整数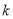 , 使
, 使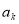 ,
, 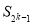 ,
, 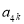 成等比数列? 若存在, 求
成等比数列? 若存在, 求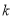 的值; 若不存在, 请说明理由.
的值; 若不存在, 请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年云南省弥勒市高三年级模拟测试一文科数学试卷(解析版) 题型:解答题
(本小题满分12分)如图,矩形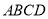 中,
中,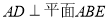 ,
,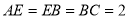 ,
,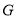 是
是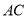 中点,
中点,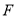 为
为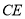 上的点,且
上的点,且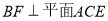 .
.

(1)求证: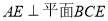 ;
;
(2)求三棱锥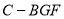 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com