
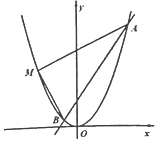
 已知抛物线x2=2py(p>0)与直线2x-y+1=0交于A,B两点,$|AB|=2\sqrt{30}$,点M在抛物线上,MA⊥MB.
已知抛物线x2=2py(p>0)与直线2x-y+1=0交于A,B两点,$|AB|=2\sqrt{30}$,点M在抛物线上,MA⊥MB.分析 (1)联立直线方程与抛物线方程,化为关于x的一元二次方程,由根与系数的关系得到A,B两点横坐标的和与积,由弦长公式求得p的值;
(2)由(1)求出A,B的坐标,设出M的坐标,利用MA⊥MB得,代入根与系数的关系求得答案.
解答 解:(1)将y=2x+1代入x2=2py,得x2-4px-2p=0,
设A(x1,y1),B(x2,y2),
则x1+x2=4p,x1x2=-2p,
由$|AB|=2\sqrt{30}$及p>0,得p=1.
(2)由(1)得设点$M({x_0},\frac{{{x_0}^2}}{2})$,$A({x_1},\frac{{{x_1}^2}}{2})$,$B({x_2},\frac{{{x_2}^2}}{2})$,
由MA⊥MB得$\overrightarrow{MA}•\overrightarrow{MB}=0$,
即$\overrightarrow{MA}=({x_1}-{x_0},\frac{{{x_1}^2-{x_0}^2}}{2})$,$\overrightarrow{MB}=({x_2}-{x_0},\frac{{{x_2}^2-{x_0}^2}}{2})$,
$\overrightarrow{MA}•\overrightarrow{MB}=({x_1}-{x_0})({x_2}-{x_0})+(\frac{{{x_1}^2-{x_0}^2}}{2})(\frac{{{x_2}^2-{x_0}^2}}{2})=0$,
∴(x1+x0)(x2+x0)+4=0,
∴${x_0}=-2±\sqrt{2}$.
点评 本题主要考查抛物线的几何性质、直线与抛物线的位置关系等基础知识,同时考查解析几何的基本思想方法和综合解题能力,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
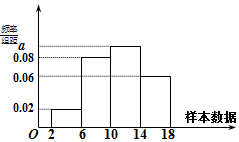 如图是容量为100的样本的频率分布直方图,其中a∈R.试根据图中的数据回答下列问题:
如图是容量为100的样本的频率分布直方图,其中a∈R.试根据图中的数据回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | -$\frac{{\sqrt{3}}}{3}$ | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{15}$ | D. | $\frac{2}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x2+2-x | B. | f(x)=x2-2-x | C. | f(x)=-x2+2-x | D. | f(x)=-x2-2-x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com