
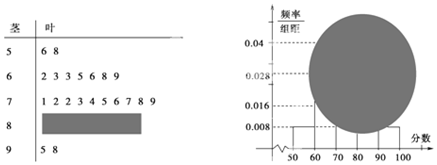
分析 (1)由茎叶图知分数在[50,60)之间的频数为2,由频率分布直方图知分数在[50,60)之间的频率为0.08,由此能求出全班人数.
(2)分数在[80,90)之间的人数为4人,分数在[80,90)之间的频率为0.16,由此能求出频率分布直方图中[90,90)间的矩形的高.
(3)将[80,90)之间的4个分数编号为1,2,3,4,[90,100]之间的2分分数编号为5,6,利用列举法能求出至少有一份分数在之间的概率.
解答 解:(1)由茎叶图知分数在[50,60)之间的频数为2,
由频率分布直方图知分数在[50,60)之间的频率为0.008×10=0.08,
∴全班人数为$\frac{2}{0.08}=25$(人).
(2)分数在[80,90)之间的人数为25-2-7-10-2=4人,
分数在[80,90)之间的频率为$\frac{4}{25}$=0.16,
∴频率分布直方图中[90,90)间的矩形的高为$\frac{0.16}{10}=0.016$.
(3)将[80,90)之间的4个分数编号为1,2,3,4,
[90,100]之间的2分分数编号为5,6,
则在[80,100]之间的试卷中任取两份的基本事件为:
(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),
(3,4),(3,5),(3,6),(4,5),(4,6),(5,6),共15个,
其中至少有一个在[90,100]之间的基本事件有:
(1,5),(1,6),(2,5),(2,6),(3,5),(3,6),(4,5),(4,6),(5,6),共15个,
∴至少有一份分数在之间的概率p=$\frac{9}{15}$=$\frac{3}{5}$.
点评 本题考查频率分布表和频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
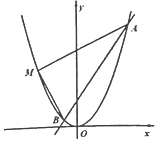 已知抛物线x2=2py(p>0)与直线2x-y+1=0交于A,B两点,$|AB|=2\sqrt{30}$,点M在抛物线上,MA⊥MB.
已知抛物线x2=2py(p>0)与直线2x-y+1=0交于A,B两点,$|AB|=2\sqrt{30}$,点M在抛物线上,MA⊥MB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com