
(本小题满分13分)某市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域近似地为半径是R的圆面.该圆面的内接四边形 是原棚户建筑用地,测量可知边界
是原棚户建筑用地,测量可知边界 万米,
万米, 万米,
万米,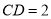 万米.
万米.

(1)请计算原棚户区建筑用地 的面积及圆面的半径
的面积及圆面的半径 的值;
的值;
(2)因地理条件的限制,边界 、
、 不能变更,而边界
不能变更,而边界 、
、 可以调整,为了提高棚户区改造建筑用地的利用率,请在圆弧
可以调整,为了提高棚户区改造建筑用地的利用率,请在圆弧 上设计一点
上设计一点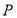 ;使得棚户区改造的新建筑用地
;使得棚户区改造的新建筑用地 的面积最大,并求最大值.
的面积最大,并求最大值.
(1)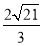 万米;(2)9
万米;(2)9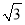 万平方米.
万平方米.
【解析】
试题分析:(1)连接AC,根据余弦定理求得cos∠ABC的值,进而求得∠ABC,然后利用三角形面积公式分别求得△ABC和△ADC的面积,二者相加即可求得四边形ABCD的面积,在△ABC中,由余弦定理求得AC,进而利用正弦定理求得外接圆的半径.
(2)设AP=x,CP=y.根据余弦定理求得x和y的关系式,进而根据均值不等式求得xy的最大值,进而求得△APC的面积的最大值,与△ADC的面积相加即可求得四边形APCD面积的最大值.
试题解析: (1)因为四边形ABCD内接于圆,
所以∠ABC+∠ADC=180°,连接AC,由余弦定理:
AC2=42+62-2×4×6×cos∠ABC=42+22-2×2×4cos∠ADC.
所以cos∠ABC=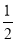 ,∵∠ABC∈(0,π),故∠ABC=60°.
,∵∠ABC∈(0,π),故∠ABC=60°.
S四边形ABCD=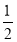 ×4×6×s1n60°+
×4×6×s1n60°+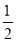 ×2×4×s1n120°
×2×4×s1n120°
=8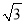 (万平方米). 3分
(万平方米). 3分
在△ABC中,由余弦定理:AC2=AB2+BC2-2AB·BC·cos∠ABC=16+36-2 4
4 6
6
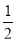 =28
=28
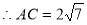
由正弦定理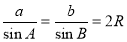 ,得
,得
 .
.
∴R=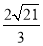 (万米) 7分
(万米) 7分
(2)∵S四边形APCD=S△ADC+S△APC,又S△ADC=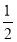 AD·CD·s1n120°=2
AD·CD·s1n120°=2 ,
,
设AP=x,CP=y.则S△APC=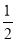 xy·s1n60°=
xy·s1n60°=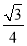 xy. 9分
xy. 9分
又由余弦定理AC2=x2+y2-2xycos60°=x2+y2-xy=28.
∴x2+y2-xy≥2xy-xy=xy.
∴xy≤28,当且仅当x=y时取等号 11分
∴S四边形APCD=2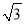 +
+ xy≤2
xy≤2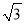 +
+ ×28=9
×28=9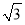 ,
,
∴最大面积为9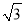 万平方米. 13分
万平方米. 13分
考点:解三角形的实际应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届辽宁省五校协作体高三上学期期中考试文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系xOy 中,曲线C1的参数方程为: (
( 为参数),M是C1上的动点,P点满足
为参数),M是C1上的动点,P点满足 ,P点的轨迹为曲线C2.
,P点的轨迹为曲线C2.
(1)求C2的方程;
(2)在以O为极点,x 轴的正半轴为极轴的极坐标系中,射线 与C1的异于极点的交点为A,与C2的异于极点的交点为B,求
与C1的异于极点的交点为A,与C2的异于极点的交点为B,求 .
.
查看答案和解析>>
科目:高中数学 来源:2015届西藏拉萨中学高三第三次月考文科数学试卷(解析版) 题型:选择题
若将函数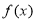 =
=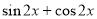 的图象向右平移
的图象向右平移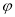
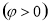 个单位,所得图象关于y轴对称,则
个单位,所得图象关于y轴对称,则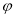 的最小值是
的最小值是
A. B.
B. C.
C.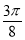 D.
D.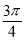
查看答案和解析>>
科目:高中数学 来源:2015届福建省福州市高三上学期第三次质检理科数学试卷(解析版) 题型:选择题
函数 (
(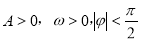 )的图象如右图所示,为了得到
)的图象如右图所示,为了得到 的图像,可以将
的图像,可以将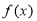 的图像
的图像

A.向左平移 个单位长度 B.向左平移
个单位长度 B.向左平移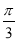 个单位长度
个单位长度
C.向右平移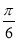 个单位长度 D.向右平移
个单位长度 D.向右平移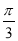 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源:2015届福建省福州市高三上学期第三次质检文科数学试卷(解析版) 题型:选择题
在实数集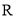 中定义一种运算“
中定义一种运算“ ”,对任意
”,对任意 ,
, 为唯一确定的实数,且具有性质:
为唯一确定的实数,且具有性质:
(1)对任意 ,
,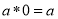 ; (2)对任意
; (2)对任意 ,
, .
.
则函数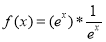 的最小值为
的最小值为
A.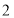 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届福建省等三校高三上学期期中联考理科数学试卷(解析版) 题型:填空题
对于函数 ,有下列4个命题:
,有下列4个命题:
①任取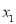 ,
,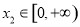 ,都有
,都有 恒成立;
恒成立;
②
 ,对于一切
,对于一切 恒成立;
恒成立;
③对任意 ,不等式
,不等式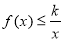 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是 .
.
④函数 有
有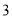 个零点;
个零点;
则其中所有真命题的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com