
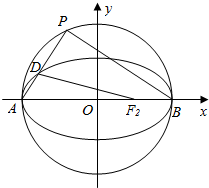
 ��֪��ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0��������Ϊ$\frac{1}{2}$��F1��F2�ֱ�Ϊ���ҽ��㣬��F1��ֱ�볤����ҳ�Ϊ3$\sqrt{2}$��
��֪��ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0��������Ϊ$\frac{1}{2}$��F1��F2�ֱ�Ϊ���ҽ��㣬��F1��ֱ�볤����ҳ�Ϊ3$\sqrt{2}$������ ��1����x=-c������Բ�ı����̿ɵã�$\frac{{c}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1�����y=��$\frac{{b}^{2}}{a}$���ɵ�$\frac{2{b}^{2}}{a}$=3$\sqrt{2}$����$\frac{c}{a}$=$\frac{1}{2}$��a2=b2+c2������������ɵó���
��2��A$��-2\sqrt{2}��0��$��B$��2\sqrt{2}��0��$��F2$��\sqrt{2}��0��$��ֱ��PB�ķ���Ϊ��$y={k}_{2}��x-2\sqrt{2}��$����ֱ��PA��б��Ϊ-$\frac{1}{{k}_{2}}$���䷽��Ϊ��y=-$\frac{1}{{k}_{2}}$��x+2$\sqrt{2}$��������Բ����������Ϊ$��3{k}_{2}^{2}+4��{x}^{2}$+16$\sqrt{2}$x+32-24${k}_{2}^{2}$=0������$-2\sqrt{2}+{x}_{D}$=$\frac{-16\sqrt{2}}{3{k}_{2}^{2}+4}$�����xD��yD����xD�١�2ʱ���ɵ�k1=$\frac{-4{k}_{2}}{{k}_{2}^{2}-4}$����Ϊ��=$\frac{4}{4-{k}_{2}^{2}}$�����ɵó���
��� 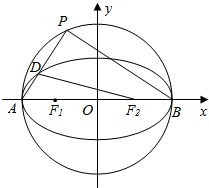 �⣺��1����x=-c������Բ�ı����̿ɵã�$\frac{{c}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1�����y=��$\frac{{b}^{2}}{a}$��
�⣺��1����x=-c������Բ�ı����̿ɵã�$\frac{{c}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1�����y=��$\frac{{b}^{2}}{a}$��
��$\frac{2{b}^{2}}{a}$=3$\sqrt{2}$����$\frac{c}{a}$=$\frac{1}{2}$��a2=b2+c2��
���������c=$\sqrt{2}$��a=2$\sqrt{2}$��b=$\sqrt{6}$��
����Բ�ı�����Ϊ$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{6}=1$��
��2��A$��-2\sqrt{2}��0��$��B$��2\sqrt{2}��0��$��F2$��\sqrt{2}��0��$��
ֱ��PB�ķ���Ϊ��$y={k}_{2}��x-2\sqrt{2}��$��
��ֱ��PA��б��Ϊ-$\frac{1}{{k}_{2}}$���䷽��Ϊ��y=-$\frac{1}{{k}_{2}}$��x+2$\sqrt{2}$����
����$\left\{\begin{array}{l}{y=-\frac{1}{{k}_{2}}��x+2\sqrt{2}��}\\{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{6}=1}\end{array}\right.$����Ϊ$��3{k}_{2}^{2}+4��{x}^{2}$+16$\sqrt{2}$x+32-24${k}_{2}^{2}$=0��
����0��
��$-2\sqrt{2}+{x}_{D}$=$\frac{-16\sqrt{2}}{3{k}_{2}^{2}+4}$��
���xD=$\frac{6\sqrt{2}{k}_{2}^{2}-8\sqrt{2}}{3{k}_{2}^{2}+4}$��yD=$\frac{-12\sqrt{2}{k}_{2}}{3{k}_{2}^{2}+4}$��
xD-$\sqrt{2}$=$\frac{6\sqrt{2}{k}_{2}^{2}-8\sqrt{2}}{3{k}_{2}^{2}+4}-\sqrt{2}$=$\frac{3\sqrt{2}{k}_{2}^{2}-12\sqrt{2}}{3{k}_{2}^{2}+4}$��
��xD�١�2ʱ��
��k1=$\frac{-12\sqrt{2}{k}_{2}}{3\sqrt{2}{k}_{2}^{2}-12\sqrt{2}}$=$\frac{-4{k}_{2}}{{k}_{2}^{2}-4}$��
��k1=��k2����$\frac{-4{k}_{2}}{{k}_{2}^{2}-4}$=��•k2��
����=$\frac{4}{4-{k}_{2}^{2}}$��
��k2��R��k2�١�2��k2��0��
��ˡʣ�-�ޣ�0���ȣ�1��+�ޣ���
���� ���⿼������Բ��Բ�ı����̼������ʡ�ֱ�ߵ�бʽ��б�ʼ��㹫ʽ�����ֱ��ֱ��б��֮��Ĺ�ϵ��������������������������������е��⣮


 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | b�Φ� | B�� | b?�� | C�� | ���� | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com