
【题目】已知函数![]() .
.
(Ⅰ)若在曲线![]() 上的一点
上的一点![]() 的切线方程为
的切线方程为![]() 轴,求此时
轴,求此时![]() 的值;
的值;
(Ⅱ)若![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)设切点![]() 的坐标为
的坐标为![]() ,根据题意得出
,根据题意得出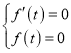 ,可求得实数
,可求得实数![]() 的值;
的值;
(Ⅱ)构造函数![]() ,求得
,求得![]() ,然后分
,然后分![]() 、
、![]() 和
和![]() 三种情况讨论,利用导数分析函数
三种情况讨论,利用导数分析函数![]() 的单调性,根据题意得出
的单调性,根据题意得出![]() ,可得出
,可得出![]() 与
与![]() 所满足的不等关系,通过构造函数,利用导数可求
所满足的不等关系,通过构造函数,利用导数可求![]() 的取值范围.
的取值范围.
(Ⅰ)设切点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() ,
,
由题意可得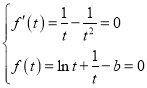 ,解得
,解得![]() ,因此,
,因此,![]() ;
;
(Ⅱ)设![]() ,则
,则![]() ,
,
①当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,令
,令![]() 得
得![]() ,所以
,所以![]() ;
;
②当![]() 时,易知
时,易知![]() 有两个根
有两个根![]() 、
、![]() ,且有
,且有![]() ,
,
不妨令![]() ,又
,又![]() ,所以
,所以![]() ,
,![]() ,由题意舍去
,由题意舍去![]() ,
,
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以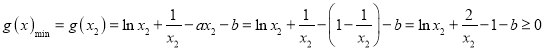 ,
,
得![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,得
,得![]() ,
,
令![]() ,则
,则![]() ,
,
令![]() ,解得
,解得![]() 或
或![]() (舍),
(舍),
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
则![]() ,所以
,所以![]() ;
;
③当![]() 时,若
时,若![]() ,取
,取![]() ,则
,则![]() ,
,
所以![]() ,不符合题意.
,不符合题意.
综上所述,![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】2020年春季,某出租汽车公同决定更换一批新的小汽车以代替原来报废的出租车,现有A,B两款车型,根据以这往这两种租车车型的数据,得到两款出租车型使用寿命频数表如表:
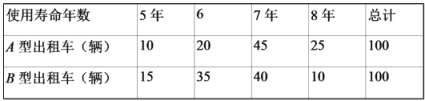
(1)填写下表,并判断是否有99%的把握认为出租车的使用寿命年数与汽车车型有关?
(2)司机师傅小李准备在一辆开了4年的A型车和一辆开了4年的B型车中选择,为了尽最大可能实现3年内(含3年)不换车,试通过计算说明,他应如何选择.
参考公式: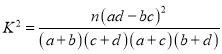 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:
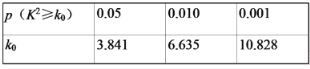
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD中,SD=CD=SC=2AB=2BC,平面ABCD⊥底面SDC,AB∥CD,∠ABC=90°,E是SD中点.
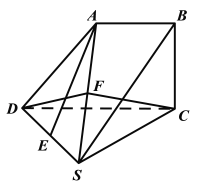
(1)证明:直线AE//平面SBC;
(2)点F为线段AS的中点,求二面角F﹣CD﹣S的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,定义:以椭圆中心为圆心,长轴为直径的圆叫做椭圆的“辅助圆”.过椭圆第四象限内一点M作x轴的垂线交其“辅助圆”于点N,当点N在点M的下方时,称点N为点M的“下辅助点”.已知椭圆E:![]() 上的点
上的点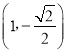 的下辅助点为(1,﹣1).
的下辅助点为(1,﹣1).
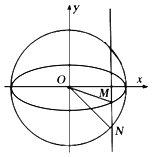
(1)求椭圆E的方程;
(2)若△OMN的面积等于![]() ,求下辅助点N的坐标;
,求下辅助点N的坐标;
(3)已知直线l:x﹣my﹣t=0与椭圆E交于不同的A,B两点,若椭圆E上存在点P,满足![]() ,求直线l与坐标轴围成的三角形面积的最小值.
,求直线l与坐标轴围成的三角形面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在1,2,3,4,5,6这六个数字所组成的允许有重复数字的三位数中,各个数位上的数字之和为9的三位数共有( )
A.16个B.18个C.24个D.25个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与椭圆
与椭圆![]() 有一个相同的焦点,过点
有一个相同的焦点,过点![]() 且与
且与![]() 轴不垂直的直线
轴不垂直的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)试问直线![]() 是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)经过点(﹣2,0)和
(a>b>0)经过点(﹣2,0)和![]() ,椭圆C上三点A,M,B与原点O构成一个平行四边形AMBO.
,椭圆C上三点A,M,B与原点O构成一个平行四边形AMBO.
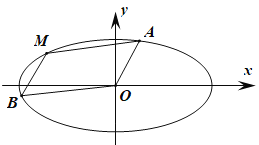
(1)求椭圆C的方程;
(2)若点B是椭圆C左顶点,求点M的坐标;
(3)若A,M,B,O四点共圆,求直线AB的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
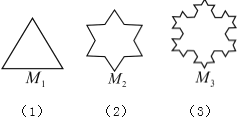
【题目】分形几何是一门以不规则几何形态为研究对象的几何学,科赫曲线是比较典型的分形图形,1904年瑞典数学家科赫第一次描述了这种曲线,因此将这种曲线称为科赫曲线.其生成方法是:(I)将正三角形(图(1))的每边三等分,以每边三等分后的中间的那一条线段为一边,向形外作等边三角形,并将这“中间一段”去掉,得到图(2);(II)将图(2)的每边三等分,重复上述的作图方法,得到图(3);(Ⅲ)再按上述方法继续做下去……,设图(1)中的等边三角形的边长为1,并且分别将图(1)、图(2)、图(3)、…、图(n)、…中的图形依次记作![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…,设
,…,设![]() 的周长为
的周长为![]() ,则
,则![]() 为( )
为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com