
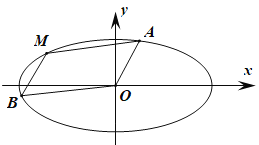
【题目】如图,在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)经过点(﹣2,0)和
(a>b>0)经过点(﹣2,0)和![]() ,椭圆C上三点A,M,B与原点O构成一个平行四边形AMBO.
,椭圆C上三点A,M,B与原点O构成一个平行四边形AMBO.
(1)求椭圆C的方程;
(2)若点B是椭圆C左顶点,求点M的坐标;
(3)若A,M,B,O四点共圆,求直线AB的斜率.
【答案】(1)![]() +y2=1;(2)M(-1,±
+y2=1;(2)M(-1,±![]() );(3)±
);(3)±![]()
【解析】
(1)将点![]() 和
和![]() 代入椭圆
代入椭圆![]() +
+![]() =1求解即可.
=1求解即可.
(2)根据平行四边形AMBO可知AM∥BO,且AM=BO=2.再设点M(x0,y0),则A(x0+2,y0),代入椭圆C求解即可.
(3) 因为A,M,B,O四点共圆,所以平行四边形AMBO是矩形,且OA⊥OB,再联立直线与椭圆的方程,结合韦达定理代入![]() ·
·![]() =x1x2+y1y2=0求解即可.
=x1x2+y1y2=0求解即可.
(1)因为椭圆![]() +
+![]() =1(a>b>0)过点
=1(a>b>0)过点![]() 和
和![]() ,
,
所以a=2,![]() +
+![]() =1,解得b2=1,所以椭圆C的方程为
=1,解得b2=1,所以椭圆C的方程为![]() +y2=1.
+y2=1.
(2)因为B为左顶点,所以B (-2,0).
因为四边形AMBO为平行四边形,所以AM∥BO,且AM=BO=2.
设点M(x0,y0),则A(x0+2,y0).
因为点M,A在椭圆C上,所以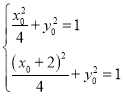 解得
解得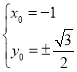 所以M(-1,±
所以M(-1,±![]() ).
).
(3)因为直线AB的斜率存在,所以设直线AB的方程为y=kx+m,A(x1,y1),B(x2,y2).
由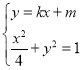 消去y,得(4k2+1)x2+8kmx+4m2-4=0,
消去y,得(4k2+1)x2+8kmx+4m2-4=0,
则有x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
因为平行四边形AMBO,所以![]() =
=![]() +
+![]() =(x1+x2,y1+y2).
=(x1+x2,y1+y2).
因为x1+x2=![]() ,所以y1+y2=k(x1+x2)+2m=k·
,所以y1+y2=k(x1+x2)+2m=k·![]() +2m=
+2m=![]() ,所以M(
,所以M(![]() ,
,![]() ).
).
因为点M在椭圆C上,所以将点M的坐标代入椭圆C的方程,化得4m2=4k2+1.①
因为A,M,B,O四点共圆,所以平行四边形AMBO是矩形,且OA⊥OB,
所以![]() ·
·![]() =x1x2+y1y2=0.
=x1x2+y1y2=0.
因为y1y2=(kx1+m)(kx1+m)=k2x1x2+km(x1+x2)+m2=![]() ,
,
所以x1x2+y1y2=![]() +
+![]() =0,化得5m2=4k2+4.②
=0,化得5m2=4k2+4.②
由①②解得k2=![]() ,m2=3,此时△>0,因此k=±
,m2=3,此时△>0,因此k=±![]() .
.
所以所求直线AB的斜率为±![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为2,过右焦点和短轴一个端点的直线的斜率为
的焦距为2,过右焦点和短轴一个端点的直线的斜率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,记
两点,记![]() 面积的最大值为
面积的最大值为![]() ,证明:
,证明: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图(如图①)、90后从事互联网行业岗位分布条形图(如图②),则下列结论中不一定正确的是( )
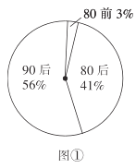
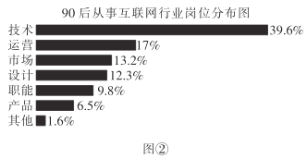
注:90后指1990年及以后出生,80后指1980~1989年之间出生,80前指1979年及以前出生.
A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的20%
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某高校全校学生的阅读情况,随机调查了200名学生每周阅读时间![]() (单位:小时)并绘制如图所示的频率分布直方图.
(单位:小时)并绘制如图所示的频率分布直方图.
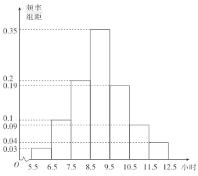
(1)求这200名学生每周阅读时间的样本平均数![]() 和中位数
和中位数![]() (
(![]() 的值精确到0.01);
的值精确到0.01);
(2)为查找影响学生阅读时间的因素,学校团委决定从每周阅读时间为![]() ,
,![]() 的学生中抽取9名参加座谈会.你认为9个名额应该怎么分配?并说明理由.
的学生中抽取9名参加座谈会.你认为9个名额应该怎么分配?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且x=0是f(x)的极值点.
,且x=0是f(x)的极值点.
(1)求f(x)的最小值;
(2)是否存在实数b,使得关于x的不等式ex<bx+f(x)在(0,+∞)上恒成立?若存在,求出b的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】七巧板是中国古代劳动人民的发明,其历史至少可以追溯到公元前一世纪,后清陆以湉《冷庐杂识》卷一中写道“近又有七巧图,其式五,其数七,其变化之式多至千余”在18世纪,七巧板流传到了国外,被誉为“东方魔板”,至今英国剑桥大学的图书馆里还珍藏着一部《七巧新谱》.完整图案为一正方形(如图):五块等腰直角三角形、一块正方形和一块平行四边形,如果在此正方形中随机取一点,那么此点取自阴影部分的概率是( )
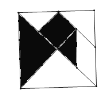
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com