
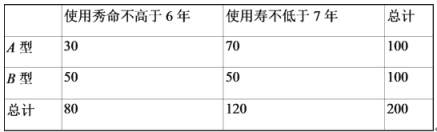
【题目】2020年春季,某出租汽车公同决定更换一批新的小汽车以代替原来报废的出租车,现有A,B两款车型,根据以这往这两种租车车型的数据,得到两款出租车型使用寿命频数表如表:
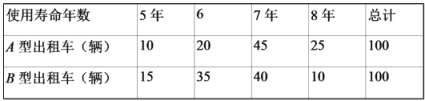
(1)填写下表,并判断是否有99%的把握认为出租车的使用寿命年数与汽车车型有关?
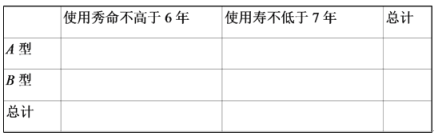
(2)司机师傅小李准备在一辆开了4年的A型车和一辆开了4年的B型车中选择,为了尽最大可能实现3年内(含3年)不换车,试通过计算说明,他应如何选择.
参考公式: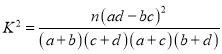 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:
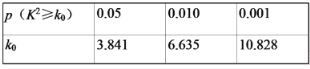
【答案】(1)填表见解析,有99%的把握认为出租车的使用寿命年数与汽车有关;(2)小李应选择A型出租车.
【解析】
(1)根据题目所给的数据填写2×2列联表,计算K的观测值K2,对照题目中的表格,得出统计结论;
(2)记事件A1,A2分别表示小李选择A型出租车和B型出租车时,3年内(含3年)换车,分别计算出P(A1)和P(A2)的值,再比较即可.
(1)根据题目所给数据得到如下2×2的列联表:
由列联表可知:K2![]() 8.33>6.635,
8.33>6.635,
所以有99%的把握认为出租车的使用寿命年数与汽车有关.
(2)记事件A1,A2分别表示小李选择A型出租车和B型出租车时,3年内(含3年)换车,
由表知:P(A1)![]() ,P(A2)
,P(A2)![]() 0.90,
0.90,
因为P(A1)<P(A2),所以小李应选择A型出租车.
【点晴】
本题考查了独立性检验的应用问题,也考查了计算能力的应用问题,属基础题.


科目:高中数学 来源: 题型:
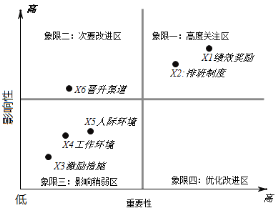
【题目】2020年1月,某公司以问卷的形式调查影响员工积极性的六项关键指标:绩效奖励、排班制度、激励措施、工作环境、人际关系、晋升渠道,在确定各项指标权重结果后,进而得到指标重要性分析象限图(如图).若客户服务中心从中任意抽取不同的两项进行分析,则这两项来自影响稍弱区的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
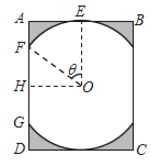
【题目】某景区修建一栋复古建筑,其窗户设计如图所示.圆![]() 的圆心与矩形
的圆心与矩形![]() 对角线的交点重合,且圆与矩形上下两边相切(
对角线的交点重合,且圆与矩形上下两边相切(![]() 为上切点),与左右两边相交(
为上切点),与左右两边相交(![]() ,
,![]() 为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1
为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1![]() ,且
,且![]() ,设
,设![]() ,透光区域的面积为
,透光区域的面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式,并求出定义域;
的函数关系式,并求出定义域;
(2)根据设计要求,透光区域与矩形窗面的面积比值越大越好.当该比值最大时,求边![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,多边形ABCDEF,四边形ABCD为等腰梯形,![]() ,
,![]() ,
,![]() ,四边形ADEF为直角梯形,
,四边形ADEF为直角梯形,![]() ,
,![]() ,以AD为折痕把等腰梯形ABCD折起,使得平面
,以AD为折痕把等腰梯形ABCD折起,使得平面![]() 平面ADEF,如图2.
平面ADEF,如图2.
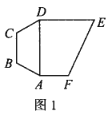
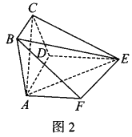
(Ⅰ)证明:![]() 平面CDE;
平面CDE;
(Ⅱ)求直线BE与平面EAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com