
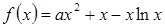 ,
,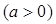
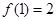 ,且在定义域内
,且在定义域内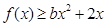 恒成立,求实数
恒成立,求实数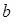 的取值范围;
的取值范围;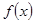 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数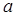 的取值范围;
的取值范围;科目:高中数学 来源:不详 题型:解答题
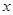 %,则销售量将减少
%,则销售量将减少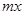 %,且该化工产品每吨的价格上涨幅度不超过
%,且该化工产品每吨的价格上涨幅度不超过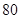 %,
%,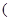 其中
其中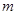 为正常数
为正常数

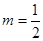 时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?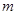 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
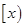 表示大于
表示大于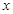 的最小整数,例如
的最小整数,例如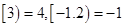 .下列命题
.下列命题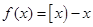 的值域是
的值域是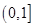 ;②若
;②若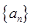 是等差数列,则
是等差数列,则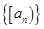 也是等差数列;
也是等差数列;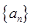 是等比数列,则
是等比数列,则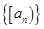 也是等比数列;④若
也是等比数列;④若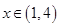 ,则方程
,则方程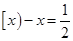 有3个根.
有3个根.| A.②④ | B.③④ | C.①③ | D.①④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
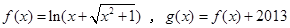 ,下列命题:
,下列命题: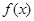 的定义域为
的定义域为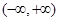 ;
; 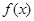 是奇函数;
是奇函数; 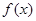 在
在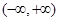 单调递增;
单调递增;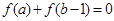 ,则
,则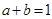 ;
;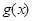 在
在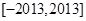 的最大值为M,最小值为m,则M+m=2013
的最大值为M,最小值为m,则M+m=2013查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
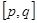 上有意义的两个函数
上有意义的两个函数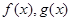 ,如果对于任意的
,如果对于任意的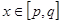 ,都有
,都有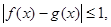 则称
则称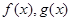 在区间
在区间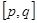 上是“接近的”两个函数,否则称它们在区间
上是“接近的”两个函数,否则称它们在区间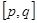 上是“非接近的”两个函数。现有两个函数
上是“非接近的”两个函数。现有两个函数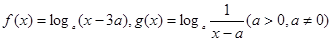 给定一个区间
给定一个区间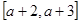 。
。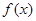 在区间
在区间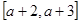 有意义,求实数
有意义,求实数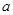 的取值范围;
的取值范围;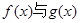 在区间
在区间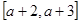 上是否是“接近的”。
上是否是“接近的”。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com