
【题目】把一枚质地均匀的骰子投掷两次,记第一次出现的点数为a,第二次出现的点数为b.已知方程组![]()
(1)求方程组只有一个解的概率;
(2)若方程组每个解对应平面直角坐标系中的点P(x,y),求点P落在第四象限的概率.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)利用列举法求出基本事件,设方程组只有一个解为事件![]() ,则事件
,则事件![]() 的对立事件是方程组无解或有无数多组解,由此利用对立事件概率计算公式能求出方程组只有一个解的概率;(2)设点
的对立事件是方程组无解或有无数多组解,由此利用对立事件概率计算公式能求出方程组只有一个解的概率;(2)设点![]() 落在第四象限为事件
落在第四象限为事件![]() ,利用列举法求出符合条件的数组的个数,由此能求出点
,利用列举法求出符合条件的数组的个数,由此能求出点![]() 落在第四象限的概率.
落在第四象限的概率.
试题解析:点(a,b)所有可能出现的结果有
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(5,1),(5,2),(5,3),(5,4)(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),共36种.
(1)“方程组![]() 只有一个解”记为事件A,其对立事件为该方程组无解或有无数多组解,则
只有一个解”记为事件A,其对立事件为该方程组无解或有无数多组解,则![]() ,即a=2b,此时有(2,1),(4,2),(6,3)3个点满足,
,即a=2b,此时有(2,1),(4,2),(6,3)3个点满足,
所以,P(A)=1-![]() .
.
(2)“点P(x,y)落在第四象限”记为事件B,
由方程组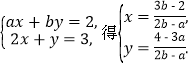 若点P落在第四象限,则有
若点P落在第四象限,则有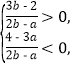
当2b-a>0,即b>![]() 时,
时,![]() 则
则![]() ,即
,即![]()
所以符合条件的点(a,b)有(2,2),(2,3),(3,2),(3,3),(3,4),(3,5),(4,2),(4,3),(4,4),(4,5),(4,6),(5,2),(5,3),(5,4),(5,5),(5,6),(6,2),(6,3),(6,4),(6,5),(6,6),共21个.当2b-a<0,即b<![]() 时,
时,![]() 则
则![]() ,不存在符合条件的点(a,b).
,不存在符合条件的点(a,b).
所以,P(B)=![]() .
.


 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:
【题目】如图, ![]() 是边长为
是边长为 ![]() 的正方形,
的正方形, ![]() 平面
平面 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 与平面
与平面 ![]() 所成角为
所成角为 ![]() .
.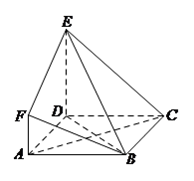
(Ⅰ)求证: ![]() 平面
平面 ![]() .
.
(Ⅱ)求二面角 ![]() 的余弦值.
的余弦值.
(Ⅲ)设点 ![]() 是线段
是线段 ![]() 上一个动点,试确定点
上一个动点,试确定点 ![]() 的位置,使得
的位置,使得 ![]() 平面
平面 ![]() ,并证明你的结论.
,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过市场调查,某种商品在销售中有如下关系:第![]() 天的销售价格(单位:元/件)为
天的销售价格(单位:元/件)为![]() ,第
,第![]() 天的销售量(单位:件)为
天的销售量(单位:件)为![]() (
(![]() 为常数),且在第20天该商品的销售收入为1200元(
为常数),且在第20天该商品的销售收入为1200元(![]() ).
).
(Ⅰ)求![]() 的值,并求第15天该商品的销售收入;
的值,并求第15天该商品的销售收入;
(Ⅱ)求在这30天中,该商品日销售收入![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】集合![]() 由满足以下性质的函数
由满足以下性质的函数![]() 组成:①
组成:①![]() 在
在![]() 上是增函数;②对于任意的
上是增函数;②对于任意的![]() ,
, ![]() .已知函数
.已知函数![]() ,
, ![]() .
.
(1)试判断![]() ,
, ![]() 是否属于集合
是否属于集合![]() ,并说明理由;
,并说明理由;
(2)将(1)中你认为属于集合![]() 的函数记为
的函数记为![]() .
.
(ⅰ)试用列举法表示集合![]() ;
;
(ⅱ)若函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,它的一个焦点到短轴顶点的距离为2,动直线l:y=kx+m交椭圆E于A、B两点,设直线OA、OB的斜率都存在,且
,它的一个焦点到短轴顶点的距离为2,动直线l:y=kx+m交椭圆E于A、B两点,设直线OA、OB的斜率都存在,且 ![]() .
.
(1)求椭圆E的方程;
(2)求证:2m2=4k2+3;
(3)求|AB|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了绿化城市,要在矩形区域ABCD内建一个矩形草坪,如图所示,另外,△AEF内部有一文物保护区不能占用,经测量AB=100 m,BC=80 m,AE=30 m,AF=20 m,应如何设计才能使草坪面积最大?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县政府为了引导居民合理用水,决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价:若用水量不超过12吨时,按4元/吨计算水费;若用水量超过12吨且不超过14吨时,超过12吨部分按6.60元/吨计算水费;若用水量超过14吨时,超过14吨部分按7.80元/吨计算水费.为了了解全市居民月用水量的分布情况,通过抽样,获得了100户居民的月用水量(单位:吨),将数据按照![]() ,
,![]() ,…,
,…,![]() 分成8组,制成了如图1所示的频率分布直方图.
分成8组,制成了如图1所示的频率分布直方图.
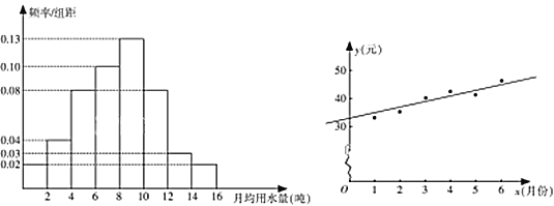
(图1) (图2)
(Ⅰ)通过频率分布直方图,估计该市居民每月的用水量的平均数和中位数(精确到0.01);
(Ⅱ)求用户用水费用![]() (元)关于月用水量
(元)关于月用水量![]() (吨)的函数关系式;
(吨)的函数关系式;
(Ⅲ)如图2是该县居民李某2017年1~6月份的月用水费![]() (元)与月份
(元)与月份![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是![]() .若李某2017年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
.若李某2017年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】相传古代印度国王在奖赏他聪明能干的宰相达依尔(国际象棋发明者)时,问他需要什么,达依尔说:“国王只要在国际象棋棋盘的第一格子上放一粒麦子,第二格子上放二粒,第三格子上放四粒,以后按比例每一格加一倍,一直放到第64格(国际象棋棋盘格数是8×8=64),我就感恩不尽,其他什么也不要了.”国王想:“这才有多少,还不容易!”于是让人扛来一袋小麦,但不到一会儿就用完了,再来一袋很快又没有了,结果全印度的粮食用完还不够,国王很奇怪,怎么也算不清这笔账.请你设计一个程序框图表示其算法,来帮国王计算一下需要多少粒小麦.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com