如果x>0,y>0,x+y+xy=2,则x+y的最小值为 .
【答案】
分析:首先分析题目已知x>0,y>0,且x+y+xy=2,求x+y的最小值.等式x+y+xy=2变形为xy=2-(x+y),根据基本不等式即可得到答案.
解答:解:已知x>0,y>0,且x+y+xy=2
即:xy=2-(x+y),
利用基本不等式:xy≤(
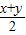
)
2.
∴2-(x+y)≤(

)
2.
解之得:x+y≥
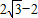
则x+y的最小值为
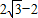
.
故答案为
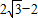
.
点评:此题主要考查基本不等式的应用问题,题中凑基本不等式是解题的关键,有一定的技巧性,但覆盖的知识点较少,属于基础题目.
