分析:(Ⅰ)连接A1B,由AB=CC1,知AB=BB1,由AA1⊥面ABCD,知AA1⊥AB.所以四边形ABB1A1为正方形.由此能够证明A1C1⊥AB.
(Ⅱ)由A1B1∥AB,知A1B1∥面ABC1.则A1到平面ABC1的距离即为B1到平面ABC1的距离.由AB⊥A1A,AB⊥A1C1,知AB⊥面AA1C1C,面ABC1⊥面AA1C1C.过A1作A1G⊥AC1于G,则A1G⊥面ABC1,则 A1G的长就是点A1到平面ABC1的距离.由此能求出点B1到平面ABC1的距离.
解答:解:(Ⅰ)证明:连接A
1B,∵AB=CC
1∴AB=BB
1又AA
1⊥面ABCD∴AA
1⊥AB
则四边形ABB
1A
1为正方形.∴AB
1⊥A
1B.∵AB
1⊥BC
1,∴AB
1⊥面A
1BC
1.∴AB
1⊥A
1C
1,∵BB
1⊥A
1C
1,∴A
1C
1⊥面A
1ABB
1,∴A
1C
1⊥AB
(Ⅱ)∵A
1B
1∥AB,∴A
1B
1∥面ABC
1.
则A
1到平面ABC
1的距离即为B
1到平面ABC
1的距离.
由( I)知,AB⊥A
1A,AB⊥A
1C
1,∴AB⊥面AA
1C
1C,∴面ABC
1⊥面AA
1C
1C.
过A
1作A
1G⊥AC
1于G,则A
1G⊥面ABC
1,
则 A
1G的长就是点A
1到平面ABC
1的距离.
在Rt△A
1B
1C
1中,A
1C
12=B
1C
12-A
1B
12=5
2-3
2=16,A
1C
1=4,
在Rt△A
1AC
1中,AC
12=A
1C
12+A
1A
2=4
2+3
2=25,AC
1=5.
则由AC
1•A
1G=AA
1•A
1C
1可得 5×A
1G=3×4,∴
A1G=故 所求距离为
.
点评:本题考查点、线、面间距离的计算,解题时要认真审题,仔细解答,注意合理地进行等价转化.

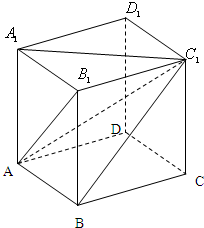 在平行六面体ABCD-A1B1C1D1中,A1A⊥面ABCD,AB1⊥BC1,AB=CC1=3,BC=5.
在平行六面体ABCD-A1B1C1D1中,A1A⊥面ABCD,AB1⊥BC1,AB=CC1=3,BC=5.

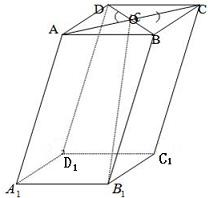
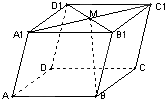 如图:在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点.若
如图:在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点.若