
(2014•宿州三模)过双曲线 (a>0,b>0)的左焦点F(﹣c,0)作圆x2+y2=a2的切线,切点为E,延长FE交抛物线y2=4cx于点P,若E为线段FP的中点,则双曲线的离心率为( )
(a>0,b>0)的左焦点F(﹣c,0)作圆x2+y2=a2的切线,切点为E,延长FE交抛物线y2=4cx于点P,若E为线段FP的中点,则双曲线的离心率为( )
A.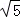 B.
B. C.
C.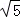 +1 D.
+1 D.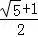
D
【解析】
试题分析:双曲线的右焦点的坐标为(c,0),利用O为FF'的中点,E为FP的中点,可得OE为△PFF'的中位线,从而可求|PF|,再设P(x,y) 过点F作x轴的垂线,由勾股定理得出关于a,c的关系式,最后即可求得离心率.
【解析】
设双曲线的右焦点为F',则F'的坐标为(c,0)
因为抛物线为y2=4cx,所以F'为抛物线的焦点
因为O为FF'的中点,E为FP的中点,所以OE为△PFF'的中位线,
属于OE∥PF'
因为|OE|=a,所以|PF'|=2a
又PF'⊥PF,|FF'|=2c 所以|PF|=2b
设P(x,y),则由抛物线的定义可得x+c=2a,
∴x=2a﹣c
过点F作x轴的垂线,点P到该垂线的距离为2a
由勾股定理 y2+4a2=4b2,即4c(2a﹣c)+4a2=4(c2﹣a2)
得e2﹣e﹣1=0,
∴e=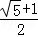 .
.
故选D.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.5直线与平面的垂直关系练习卷(解析版) 题型:?????
(2014•嘉兴一模)如图1,在等腰△ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点,CD=BE=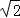 ,O为BC的中点.将△ADE沿DE折起,得到如图2所示的四棱锥A′﹣BCDE.若A′O⊥平面BCDE,则A′D与平面A′BC所成角的正弦值等于( )
,O为BC的中点.将△ADE沿DE折起,得到如图2所示的四棱锥A′﹣BCDE.若A′O⊥平面BCDE,则A′D与平面A′BC所成角的正弦值等于( )
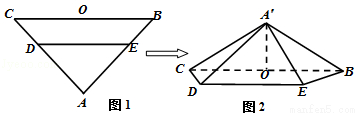
A.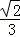 B.
B.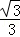 C.
C.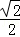 D.
D.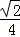
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.2空间中向量的概念和运算练习卷(解析版) 题型:?????
(2009•杭州二模)已知空间任一点O和不共线的三点A,B,C,满足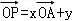
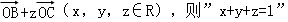 是“点P位于平面ABC内”的( )
是“点P位于平面ABC内”的( )
A.充分但不必要条件
B.必要但不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.1尝试用向量处理空间图形练习卷(解析版) 题型:?????
已知正方体ABCD﹣A′B′C′D′中,点F是侧面CDD′C′的中心,若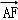 =
=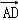 +x
+x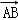 +y
+y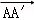 ,则x﹣y等于( )
,则x﹣y等于( )
A.0 B.1 C. D.﹣
D.﹣
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 2.4圆锥曲线的应用练习卷(解析版) 题型:?????
(2014•河池一模)已知椭圆的一个焦点为F,若椭圆上存在点P,满足以椭圆短轴为直径的圆与线段PF相切于线段PF的中点,则该椭圆的离心率为( )
A. B.
B.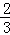 C.
C.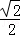 D.
D.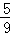
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 2.4圆锥曲线的应用练习卷(解析版) 题型:?????
(2014•淄博三模)过抛物线y2=8x的焦点作直线L交抛物线于A、B两点,若线段AB的中点的横坐标为4,则|AB|等于( )
A.14 B.12 C.10 D.8
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 2.4圆锥曲线的应用练习卷(解析版) 题型:?????
(2014•芜湖模拟)双曲线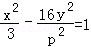 (p>0)的左焦点在抛物线y2=2px的准线上,则该双曲线的离心率为( )
(p>0)的左焦点在抛物线y2=2px的准线上,则该双曲线的离心率为( )
A.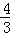 B.
B.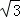 C.
C.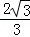 D.4
D.4
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 7.4副数的几何表示练习卷(解析版) 题型:?????
(2014•重庆)在复平面内复数Z=i(1﹣2i)对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 7.2复数的概念练习卷(解析版) 题型:?????
(2015•南充一模)已知复数z=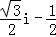 ,则z的共轭复数为( )
,则z的共轭复数为( )
A.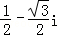 B.
B.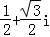 C.
C.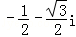 D.
D.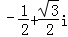
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com