
(2009•杭州二模)已知空间任一点O和不共线的三点A,B,C,满足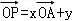
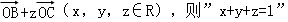 是“点P位于平面ABC内”的( )
是“点P位于平面ABC内”的( )
A.充分但不必要条件
B.必要但不充分条件
C.充要条件
D.既不充分也不必要条件
C
【解析】
试题分析:要寻求四点A、B、C、D共面的充要条件,自然想到共面向量定理.用 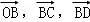 表示出
表示出 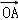 ,进而用
,进而用  表示
表示 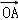 ,三者的系数之和为1即可找出答案.
,三者的系数之和为1即可找出答案.
【解析】
已知空间任一点O和不共线的三点A,B,C,满足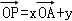
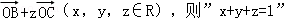 是“点P位于平面ABC内”的充要条件.证明如下:
是“点P位于平面ABC内”的充要条件.证明如下:
(必要性)依题意知,B、C、D三点不共线,
则由共面向量定理的推论知:四点A、B、C、D共面
?对空间任一点O,存在实数x1、y1,使得  =
=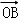 +x1
+x1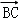 +y1
+y1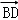
=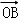 +x1(
+x1( 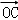 ﹣
﹣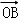 )+y1(
)+y1( 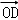 ﹣
﹣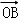 )
)
=(1﹣x1﹣y1)  +x1
+x1 +y1
+y1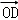 ,
,
取x=1﹣x1﹣y1、y=x1、z=y1,
则有 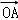 =x
=x  +y
+y  +z
+z 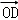 ,且x+y+z=1.
,且x+y+z=1.
(充分性)对于空间任一点O,存在实数x、y、z且x+y+z=1,使得 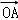 =x
=x 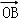 +y
+y 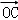 +z
+z 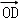 .
.
所以x=1﹣y﹣z得 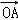 =(1﹣y﹣z)
=(1﹣y﹣z) 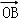 +y
+y 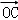 +z
+z 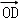 .
.
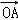 =
=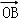 +y
+y 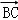 +z
+z 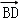 ,即:
,即: ,
,
所以四点A、B、C、D共面.
所以,空间任意无三点共线的四点A、B、C、D共面的充分必要条件是:
对于空间任一点O,存在实数x、y、z且x+y+z=1,使得 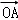 =x
=x 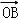 +y
+y 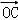 +z
+z 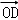 .
.
故选C.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.9共面与平行练习卷(解析版) 题型:?????
设两不同直线a,b的方向向量分别是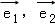 ,平面α的法向量是
,平面α的法向量是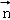 ,
,
则下列推理①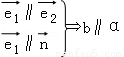 ;②
;②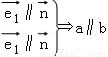 ;③
;③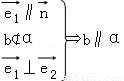 ; ④
; ④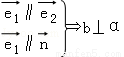 ;
;
其中正确的命题序号是( )
A.①②③ B.②③④ C.①③④ D.①②④
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.2空间中向量的概念和运算练习卷(解析版) 题型:?????
设 =(x,4,3),
=(x,4,3), =(3,2,z),且
=(3,2,z),且 ∥
∥ ,则xz的值为( )
,则xz的值为( )
A.9 B.﹣9 C.4 D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.2空间中向量的概念和运算练习卷(解析版) 题型:?????
已知点A(﹣3,1,﹣4),则点A关于x轴的对称点的坐标为( )
A.(﹣3,﹣1,4) B.(﹣3,﹣1,﹣4) C.(3,1,4) D.(3,﹣1,﹣4)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.1尝试用向量处理空间图形练习卷(解析版) 题型:?????
已知点P为三棱锥O﹣ABC的底面ABC所在平面内的一点,且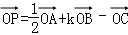 ,则实数k的值为( )
,则实数k的值为( )
A. B.
B. C.1 D.
C.1 D.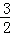
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.1尝试用向量处理空间图形练习卷(解析版) 题型:?????
(理) 在长方体ABCD﹣A1B1C1D1中,以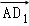 ,
,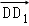 ,
,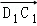 为基底表示
为基底表示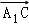 ,其结果是( )
,其结果是( )
A.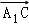 =
=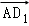 +
+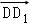 +
+
B.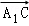 =
=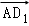
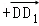

C. =
=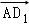 ﹣2
﹣2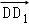 +
+
D.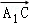 =
=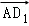
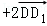
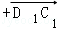
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 2.4圆锥曲线的应用练习卷(解析版) 题型:?????
(2014•宿州三模)过双曲线 (a>0,b>0)的左焦点F(﹣c,0)作圆x2+y2=a2的切线,切点为E,延长FE交抛物线y2=4cx于点P,若E为线段FP的中点,则双曲线的离心率为( )
(a>0,b>0)的左焦点F(﹣c,0)作圆x2+y2=a2的切线,切点为E,延长FE交抛物线y2=4cx于点P,若E为线段FP的中点,则双曲线的离心率为( )
A.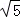 B.
B. C.
C.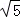 +1 D.
+1 D.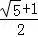
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com