已知直线l:x+y-6=0和圆M:x2+y2-2x-2y-2=0,点A在直线l上,若直线AC与圆M至少有一个公共点C,且∠MAC=30°,则点A的横坐标的取值范围是( )
A.(0,5)
B.[1,5]
C.[1,3]
D.(0,3]
【答案】
分析:设点A的坐标为(x
,6-x
),圆心M到直线AC的距离为d,则d=|AM|sin30°,由直线AC与⊙M有交点,知d=|AM|sin30°≤2,由此能求出点A的横坐标的取值范围.
解答:解:
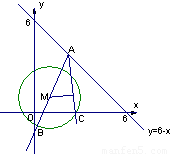
如图,设点A的坐标为(x
,6-x
),
圆心M到直线AC的距离为d,
则d=|AM|sin30°,
∵直线AC与⊙M有交点,
∴d=|AM|sin30°≤2,
∴(x
-1)
2+(5-x
)
2≤16,
∴1≤x
≤5,
故选B.
点评:本题考查直线和圆的方程的综合运用,是基础题.解题时要认真审题,注意数形结合思想的灵活运用.

 阅读快车系列答案
阅读快车系列答案