
如图,矩形 所在的半平面和直角梯形
所在的半平面和直角梯形 所在的半平面成
所在的半平面成 的二面角,
的二面角, ∥
∥ ,
, ,
, ,
, ,
, ,
, .
.
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)在线段 上求一点
上求一点 ,使锐二面角
,使锐二面角 的余弦值为
的余弦值为 .
.

(Ⅰ)因为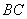 ∥
∥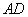 ,
,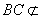 平面
平面 ,所以
,所以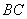 ∥平面
∥平面 ,
,
同理 ∥平面
∥平面 ,又因为
,又因为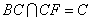 ,所以平面
,所以平面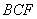 ∥平面
∥平面 ,
,
而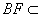 平面
平面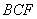 ,所以
,所以 ∥平面
∥平面 . ………………………………………5分
. ………………………………………5分
(Ⅱ)因为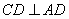 ,
, 所以
所以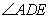 就是二面角
就是二面角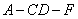 的平面角,为
的平面角,为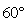 , ……………………………………………………………………………………6分
, ……………………………………………………………………………………6分
又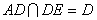 ,所以
,所以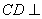 平面
平面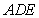 ,平面
,平面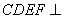 平面
平面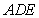 ,
,
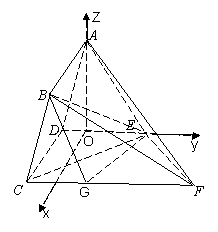 作
作 于
于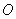 ,则
,则 ,…………7分
,…………7分
连结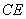 ,在
,在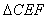 中由余弦定理求得
中由余弦定理求得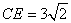 ,
,
易求得, ,
,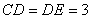 ,
, ,
,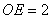 . ……………………………………………8分
. ……………………………………………8分
以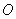 为原点,以平行于
为原点,以平行于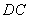 的直线为
的直线为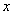 轴,以直线
轴,以直线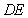 为
为
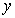 轴,建立如图空间直角坐标系
轴,建立如图空间直角坐标系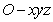 ,
,
则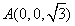
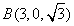 ,
,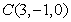 ,
,
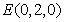 ,
,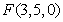 ,
,
设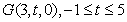 ,
,
则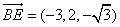 ,
,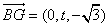 ,
,
设平面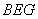 的一个法向量为,
的一个法向量为,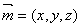 ,
,
则由 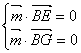 得,
得,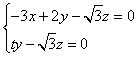 ,
,
取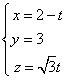 得,
得, 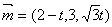 , …………………………………………10分
, …………………………………………10分
平面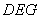 的一个法向量
的一个法向量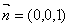 , …………………………………………11分
, …………………………………………11分
所以,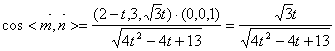 , ………12分
, ………12分
为使锐二面角 的余弦值为
的余弦值为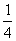 ,只需
,只需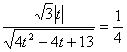 ,
,
解得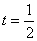 ,此时
,此时 , …………………………………………………13分
, …………………………………………………13分
即所求的点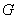 为线段
为线段 的靠近
的靠近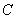 端的四分之一分点. …………………………14分
端的四分之一分点. …………………………14分


科目:高中数学 来源: 题型:
下列说法正确的是 .(只填序号)
① 函数 的图象与直线
的图象与直线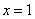 的交点个数为0或1;
的交点个数为0或1;
② “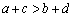 ”是“
”是“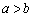 且
且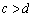 ”的充分而不必要条件;
”的充分而不必要条件;
③ 命题“存在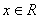 ,使得
,使得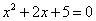 ”的否定是“对任意
”的否定是“对任意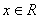 ,都有
,都有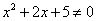 ”.
”.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知有公共焦点的椭圆与双曲线中心为原点,焦点在 轴上,左、右焦点分别为
轴上,左、右焦点分别为 ,且它们在第一象限的交点为
,且它们在第一象限的交点为 ,
, 是以
是以 为底边的等腰三角形,若双曲线的离心率的取值范围为
为底边的等腰三角形,若双曲线的离心率的取值范围为 .则该椭圆的离心率的取值范围是 .
.则该椭圆的离心率的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com