Question

两类药片有效成分如下表:

成分 药品	阿斯匹林(mg)	小苏打(mg)	可待因(mg)	每片价格(元)
A(1片)	2	5	1	0.1
B(1片)	1	7	6	0.2

若要求至少提供12 mg阿斯匹林,70 mg小苏打,28 mg可待因,两类药片的最小总数是多少?怎样搭配价值最低?

Answer 1

解：设需用A和B两种药品各为x片和y片,药品总数为z(片),价格搭配为L(元).

则由题意,得约束条件

线性目标函数为

药品总数z=x+y,

搭配价格L=0.1x+0.2y.

由不等式组作可行域,如图.

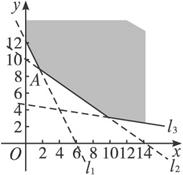
l₁:2x+y=12,l₂:5x+7y=70,l₃:x+6y=28.

而k₁=-2,k₂=-,k₃=-.

直线l:x+y=t,k_l=-1.

有k₁＜k_l＜k₂.

故直线l:x+y=z,过l₁与l₂的交点A时,z有最小值.

解方程组得交点A(,).

然而点A不是整点,故不能作为最优解,此时,过点A的直线为l_A:x+y=.

可行域内与直线l_A距离最近的整点有(1,10)、(2,9)、(3,8),使z_min=11,即药品的总数为11.

而最低搭配价格L_min=(0.1x+0.2y)_min为

L₁=0.1×1+0.2×10=2.1,

L₂=0.1×2+0.2×9=2.0,

L₃=0.1×3+0.2×8=1.9

中的最小者,所以L_min=1.9(元).

所以药品为11片,其中3片A种药,8片B种药的搭配价最低.