
【题目】某厂家拟在2010年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)x万件与年促销费用m万元(m≥0)满足x=3﹣ ![]() (k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2010年该产品的利润y万元表示为年促销费用m万元的函数;
(2)该厂家2010年的促销费用投入多少万元时,厂家的利润最大.
【答案】
(1)解:由题意可知当m=0时,x=1(万件),
∴1=3﹣kk=2.
∴x=3﹣ ![]() .
.
每件产品的销售价格为1.5× ![]() (元),
(元),
∴2010年的利润y=x ![]() ﹣(8+16x+m)
﹣(8+16x+m)
=4+8x﹣m=4+8 ![]() ﹣m
﹣m
=﹣ ![]() +29(m≥0)
+29(m≥0)
(2)解:∵m≥0时, ![]() +(m+1)≥2
+(m+1)≥2 ![]() =8,
=8,
∴y≤﹣8+29=21,当且仅当 ![]() =m+1m=3(万元)时,
=m+1m=3(万元)时,
ymax=21(万元).
所以当该厂家2010年的促销费用投入3万元时,厂家的利润最大
【解析】(1)由题意可知当m=0时,x=1由满足x=3﹣ ![]() ,即可得出k值,从而得出每件产品的销售价格,从而得出2010年的利润的表达式即可;(2)对于(1)中求得的解析式,根据其中两项之积为定值结合利用基本不等式此函数的最大值及相应的x值,从而解决该厂家2010年的促销费用投入多少万元时,厂家的利润最大.
,即可得出k值,从而得出每件产品的销售价格,从而得出2010年的利润的表达式即可;(2)对于(1)中求得的解析式,根据其中两项之积为定值结合利用基本不等式此函数的最大值及相应的x值,从而解决该厂家2010年的促销费用投入多少万元时,厂家的利润最大.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() 是椭圆E:
是椭圆E:![]() (a>b>0)上一点,离心率为
(a>b>0)上一点,离心率为![]() .
.
(1)求椭圆E的方程;
(2)设不过原点O的直线l与该椭圆E交于P,Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,求△OPQ面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数{an}满a1=0,an+1=an+2n,那a2016的值是( )
A.2014×2015
B.2015×2016
C.2014×2016
D.2015×2015
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中的“两鼠穿墙题”是我国数学的古典名题:“今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半,问何日相逢,各穿几何?”题意是:“有两只老鼠从墙的两边打洞穿墙,大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半.”如果墙足够厚,![]() 为前
为前![]() 天两只老鼠打洞之和,则
天两只老鼠打洞之和,则![]() _________________尺.
_________________尺.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个无穷数列![]() 和
和![]() 的前
的前![]() 项和分别为
项和分别为![]() ,
,![]() ,
,![]() ,
,![]() ,对任意的
,对任意的![]() ,都有
,都有![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() 为等差数列,对任意的
为等差数列,对任意的![]() ,都有
,都有![]() .证明:
.证明:![]() ;
;
(3)若![]() 为等比数列,
为等比数列,![]() ,
,![]() ,求满足
,求满足![]() 的
的![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设(x1 , y1),(x2 , y2),…,(xn , yn),是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是( ) 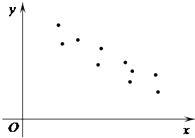
A.x和y正相关
B.x和y的相关系数为直线l的斜率
C.x和y的相关系数在﹣1到0之间
D.当n为偶数时,分布在l两侧的样本点的个数一定相同
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂用甲、乙两种不同工艺生产一大批同一种零件,零件尺寸均在[21.7,22.3](单位:cm)之间,把零件尺寸在[21.9,22.1)的记为一等品,尺寸在[21.8,21.9)∪[22.1,22.2)的记为二等品,尺寸在[21.7,21.8)∪[22.2,22.3]的记为三等品,现从甲、乙工艺生产的零件中各随机抽取100件产品,所得零件尺寸的频率分布直方图如图所示.
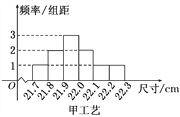
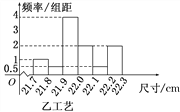
P(K2≥k0) | 0.10 | 0.05 | 0.01 |
k0 | 2.706 | 3.841 | 6.635 |
附: 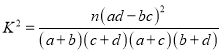
(1)根据上述数据完成下列2×2列联表,根据此数据,你认为选择不同的工艺与生产出一等品是否有关?
甲工艺 | 乙工艺 | 总计 | |
一等品 | |||
非一等品 | |||
总计 |
(2)以上述各种产品的频率作为各种产品发生的概率,若一等品、二等品、三等品的单件利润分别为30元、20元、15元,你认为以后该工厂应该选择哪种工艺生产该种零件?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com