
| A. | $({-∞,-1}]∪[{0,2\sqrt{2}-1}]$ | B. | $[{-1,2\sqrt{2}-1}]$ | C. | (-∞,-1]∪(0,3] | D. | [-1,3] |
分析 先将不等式转化为g(a)≥-2,再根据函数的解析式,分类求解.
解答 解:设x>0,则-x<0,g(x)=-g(-x)=-x2-2x+5,
由题意,a<0,a2+a=2,∴a=-2,
∵f(g(a))≤2,$f(x)=\left\{\begin{array}{l}{x^2}+x,x<0\\-{x^2},x≥0\end{array}\right.$,∴g(a)≥-2,
∴$\left\{\begin{array}{l}{a<0}\\{{a}^{2}-2a-5≥-2}\end{array}\right.$或$\left\{\begin{array}{l}{a>0}\\{-{a}^{2}-2a+5≥-2}\end{array}\right.$或a=0,
∴a≤-1或0≤a≤2$\sqrt{2}$-1,
故选A.
点评 本题考查不等式的解法,考查函数的性质,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | [0,1] | C. | (1,3) | D. | [1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow a•\overrightarrow b=2$ | B. | $\overrightarrow a∥\overrightarrow b$ | C. | $|\overrightarrow a|=|\overrightarrow b|$ | D. | $\overrightarrow b⊥(\overrightarrow a+\overrightarrow b)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $-\frac{4}{3}$ | D. | $-\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
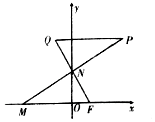 已知点F(1,0),动点M,N分别在x轴,y轴上运动,MN⊥NF,Q为平面上一点,$\overrightarrow{NQ}+\overrightarrow{NF}=\overrightarrow 0$,过点Q作QP平行于x轴交MN的延长线于点P.
已知点F(1,0),动点M,N分别在x轴,y轴上运动,MN⊥NF,Q为平面上一点,$\overrightarrow{NQ}+\overrightarrow{NF}=\overrightarrow 0$,过点Q作QP平行于x轴交MN的延长线于点P.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,3] | B. | [3,5] | C. | [5,7] | D. | [7,9] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com